题目内容
14.一水果商为了获得更多利润,对往年销售某水果情况进行了统计,得到如表的数据:| 销售价x(元/千克) | … | 25 | 24 | 23 | 22 | … |
| 销售量y(千克) | … | 2000 | 2500 | 3000 | 3500 | … |
(2)若该水果进价为13元/千克,设销售利润为W(元);试求销售利润W(元)与销售价x(元/千克)之间的函数关系式,求当x取何值时,销售利润最大?
分析 (1)设出函数解析式,进一步代入求得函数解析式;
(2)利用销售利润=每千克的利润×销售量求得函数解析式,根据函数性质求最值.
解答 解:设y=kx+b,
∵点(25,2000),(24,2500)在图象上,
∴$\left\{\begin{array}{l}{2000=25k+b}\\{2500=24k+b}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-500}\\{b=14500}\end{array}\right.$.
∴y=-500x+14500.
(2)W=(x-13)•y
=(x-13)•(-500x+14500)
=-500x2+21000x-188500
=-500(x-21)2+32000.
P与x的函数关系式为:P=-500x2+21000x-188500,
当销售价为21元/千克时,W的值最大为32000.
点评 此题考查二次函数的实际运用,掌握待定系数法求函数解析式,二次函数的性质以及基本的数量关系是解决问题的关键.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
5. 如图,在3×3的正方形网格中,含有“梦”字的正方形的个数是( )
如图,在3×3的正方形网格中,含有“梦”字的正方形的个数是( )
 如图,在3×3的正方形网格中,含有“梦”字的正方形的个数是( )
如图,在3×3的正方形网格中,含有“梦”字的正方形的个数是( )| A. | 1个 | B. | 4个 | C. | 6个 | D. | 14个 |
3.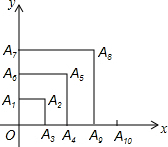 如图,有一系列有规律的点,它们分别是以O为顶点,边长为正整数的正方形的顶点:A1(0,1),A2(1,1),A3(1,0),A4(2,0),A5(2,2),A6(0,2),A7(0,3),A8(3,3),…,依此规律,点A2016的坐标为( )
如图,有一系列有规律的点,它们分别是以O为顶点,边长为正整数的正方形的顶点:A1(0,1),A2(1,1),A3(1,0),A4(2,0),A5(2,2),A6(0,2),A7(0,3),A8(3,3),…,依此规律,点A2016的坐标为( )
 如图,有一系列有规律的点,它们分别是以O为顶点,边长为正整数的正方形的顶点:A1(0,1),A2(1,1),A3(1,0),A4(2,0),A5(2,2),A6(0,2),A7(0,3),A8(3,3),…,依此规律,点A2016的坐标为( )
如图,有一系列有规律的点,它们分别是以O为顶点,边长为正整数的正方形的顶点:A1(0,1),A2(1,1),A3(1,0),A4(2,0),A5(2,2),A6(0,2),A7(0,3),A8(3,3),…,依此规律,点A2016的坐标为( )| A. | (0,672) | B. | (671,671) | C. | (672,672) | D. | (672,0) |
4.已知△ABC两边长度分别是3cm,4cm,则连结各边中点的三角形的周长可能为( )
| A. | 3.5cm | B. | 12cm | C. | 6.4cm | D. | 10cm |
 如图,AB是⊙O的直径,AC是弦,D是$\widehat{AC}$的中点,DE⊥AB于E,DF交AC于按F,DB交AC于点G.下面结论:①FA=FD=FG;②FG=GC;③CD是DG与DB的比例中项;④$\frac{EO}{OB}$=$\frac{EF}{FD}$,其中正确的结论有3个.
如图,AB是⊙O的直径,AC是弦,D是$\widehat{AC}$的中点,DE⊥AB于E,DF交AC于按F,DB交AC于点G.下面结论:①FA=FD=FG;②FG=GC;③CD是DG与DB的比例中项;④$\frac{EO}{OB}$=$\frac{EF}{FD}$,其中正确的结论有3个.
 用一段长24m的篱笆围成一个一边靠墙的矩形菜园,墙长为15m,这个矩形长、宽各为多少时,菜园面积最大,最大面积是多少?
用一段长24m的篱笆围成一个一边靠墙的矩形菜园,墙长为15m,这个矩形长、宽各为多少时,菜园面积最大,最大面积是多少?