题目内容
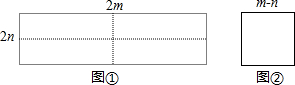
2.如图①所示是一个长为2m,宽为2n的长方形,沿图中虚线用剪刀均分成四个小长方形,图②是边长为m-n的正方形.(1)请用图①中四个小长方形和图②中的正方形拼成一个大正方形,画出示意图(要求连接处既没有重叠,也没有空隙);
(2)请用两种不同的方法列代数式表示(1)中拼得的大正方形的面积.
方法1:(m-n)2+2m•2n=(m+n)2,方法2(m+n)(m-n)=(m+n)2.
(3)请直接写出(m+n)2,(m-n)2,mn这三个代数式之间的等量关系.
(4)根据(3)题中的等量关系,解决如下问题:若a+b=6,ab=4,则求(a-b)2的值.
分析 (1)求出大正方形的面积,即可得到大正方形的边长,根据边长画出图形即可;
(2)从部分和整体两个角度求大正方形的面积即可;
(3)根据第(2)小题的结论,直接写出结论即可;
(4)利用(3)中的结论,直接代数求值即可.
解答  解:(1)如右图:
解:(1)如右图:
(2)方法1:(m-n)2+2m•2n=m2-2mn+n2+4mn=m2+2mn+n2=(m+n)2,
方法2:(m+n)•(m+n)=(m+n)2;
故答案为:(m-n)2+2m•2n=(m+n)2,(m+n)•(m+n)=(m+n)2.
点评 本题主要考查了完全平方公式的几何背景,能从整体和部分两个角度求出图形的面积是解决此题的关键.

练习册系列答案
相关题目
13.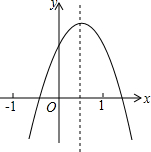 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,给出以下结论,其中正确的是( )
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,给出以下结论,其中正确的是( )
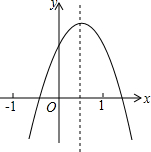 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,给出以下结论,其中正确的是( )
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,给出以下结论,其中正确的是( )| A. | a>0 | B. | b<0 | C. | c<0 | D. | a-b+c<0 |
14.一水果商为了获得更多利润,对往年销售某水果情况进行了统计,得到如表的数据:
(1)已知y是x的一次函数,请同学们根据表中数据求出y与x之间的函数关系式;
(2)若该水果进价为13元/千克,设销售利润为W(元);试求销售利润W(元)与销售价x(元/千克)之间的函数关系式,求当x取何值时,销售利润最大?
| 销售价x(元/千克) | … | 25 | 24 | 23 | 22 | … |
| 销售量y(千克) | … | 2000 | 2500 | 3000 | 3500 | … |
(2)若该水果进价为13元/千克,设销售利润为W(元);试求销售利润W(元)与销售价x(元/千克)之间的函数关系式,求当x取何值时,销售利润最大?
 已知△ABC的三个顶点的坐标分别是A(-4,0),B(2,0),C(-5,4).
已知△ABC的三个顶点的坐标分别是A(-4,0),B(2,0),C(-5,4).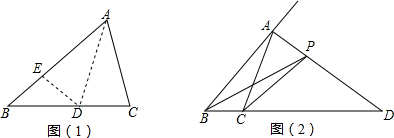
 已知:如图,直线AB与CD交于点O,OE⊥CD,OF⊥AB,∠BOD=25°,
已知:如图,直线AB与CD交于点O,OE⊥CD,OF⊥AB,∠BOD=25°,