题目内容
16．不等式2x＜a的解都满足不等式x＜2，求a的取值范围．分析 根据解不等式，可得不等式的解集，根据不等式的解集满足不等式x＜2，可得答案．
解答 解：2x＜a解得x＜$\frac{a}{2}$，
2x＜a的解都满足不等式x＜2，
$\frac{a}{2}$≤2，
解得a≤4．
点评 本题考查了不等式的解集，利用不等式的解集得出$\frac{a}{2}$＜2是解题关键．
练习册系列答案
相关题目
6．平面上有相距2cm的A，B两点，以AB为一边作面积为2cm2的等腰三角形，最多能作（ ）
| A． | 2个 | B． | 4个 | C． | 6个 | D． | 10个 |
有一块长方体的水泥砖（如图所示），不借助于任何其他仪器，不经任何计算，利用笔和长度足够的刻度尺，测出长方体内最长的直线距离．
4．“十一”黄金周期间，某风景区在7天假期中，每天旅游的人数变化如下表（正数表示比前一天增加的人数，负数表示比前一天减少的人数）所示（单位：万人），若9月30日的游客人数为1万人．
（1）这7天内哪天游客的人数最多？哪天游客的人数最少？
（2）这7天内该风景区平均每天有游客多少人？
| 人数 | 1日 | 2日 | 3日 | 4日 | 5日 | 6日 | 7日 |
| 人数变化 | +1.6 | +0.8 | +0.4 | -0.4 | -0.8 | +0.2 | -1.2 |
（2）这7天内该风景区平均每天有游客多少人？
8．通过计算填写下表：
请你根锯上表，直接写出a2+$\frac{1}{{a}^{2}}$与（a+$\frac{1}{a}$）2之间的数量关系；并验证当a=-$\frac{1}{2}$时，你得到的数量关系是否还成立．
| a | 2 | -$\frac{1}{3}$ | -1 |
| a2+$\frac{1}{{a}^{2}}$ | $\frac{17}{4}$ | $\frac{82}{9}$ | 2 |
| （a+$\frac{1}{a}$）2 | $\frac{25}{4}$ | $\frac{100}{9}$ | 4 |
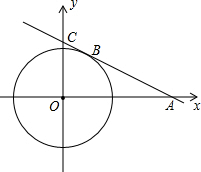如图，直线y=-$\frac{\sqrt{3}}{3}$x+$\frac{2\sqrt{3}}{3}$交坐标轴于A、C两点，且半径为1的⊙O有公共点B，问：