题目内容
11.已知a、b互为相反数且b≠0,c、d的互为倒数,m的绝对值是最小的正整数,求m-$\frac{a}{b}$+$\frac{2007(a+b)}{2008}$-cd的值.分析 a、b互为相反数且b≠0,c、d互为倒数,m的绝对值是最小的正整数,可分别求得a+b=0,cd=1,m=1,且$\frac{a}{b}$=-1,代入求值即可.
解答 解:∵a、b互为相反数且b≠0,c、d的互为倒数,m的绝对值是最小的正整数,
∴a+b=0,cd=1,m=1,且$\frac{a}{b}$=-1,
∴m-$\frac{a}{b}$+$\frac{2007(a+b)}{2008}$-cd=1+1-1=1.
点评 此题考查代数式求值,倒数、相反数、绝对值的有关概念,解题的关键是由条件求得a+b=0,cd=1,m=1.

练习册系列答案
相关题目
19.某人画二次函数y=ax2+bx+c的图象时,列出下表(计算没有错误):
根据此表判断:一元二次方程ax2+bx+c=0的一个根x1满足下列关系式( )
| X | 3.2 | 3.3 | 3.4 | 3.5 |
| y | -0.56 | -0.17 | 0.08 | 0.44 |
| A. | 3.2<x1<3.3 | B. | 3.3<x1<3.4 | C. | 3.4<x1<3.5 | D. | 3.1<x1<3.2 |
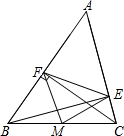 如图,△ABC中,BE⊥AC,CF⊥AB,垂足分别为E、F,M为BC的中点.
如图,△ABC中,BE⊥AC,CF⊥AB,垂足分别为E、F,M为BC的中点.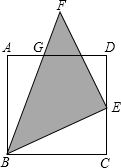 如图,点E是正方形ABCD的CD边上的一点,以BE为一条直角边作等腰直角三角形BEF,斜边BF交AD于G,已知AG=5厘米,GD=15厘米.三角形BEF的面积是272厘米2.
如图,点E是正方形ABCD的CD边上的一点,以BE为一条直角边作等腰直角三角形BEF,斜边BF交AD于G,已知AG=5厘米,GD=15厘米.三角形BEF的面积是272厘米2. 有理数a,b,c在数轴上的对应点如图所示,化简:|a+b|+|c+b|+|c-a|.
有理数a,b,c在数轴上的对应点如图所示,化简:|a+b|+|c+b|+|c-a|.