题目内容
4.“十一”黄金周期间,某风景区在7天假期中,每天旅游的人数变化如下表(正数表示比前一天增加的人数,负数表示比前一天减少的人数)所示(单位:万人),若9月30日的游客人数为1万人.| 人数 | 1日 | 2日 | 3日 | 4日 | 5日 | 6日 | 7日 |
| 人数变化 | +1.6 | +0.8 | +0.4 | -0.4 | -0.8 | +0.2 | -1.2 |
(2)这7天内该风景区平均每天有游客多少人?
分析 (1)根据有理数的加法,可得答案;
(2)根据总人数除以时间,可得答案.
解答 解:(1)1日1+1.6=2.6万,2日2.6+0.8=3.4万,3日3.4+0.4=3.8万,4日3.8-0.4=3万,5日3-0.8=2.2万,6日2.2+0.2=2.4万,7日2.4-1.2=1.2万,
3日游客人数最多,7日游客人数最少;
(2)(2.6+3.4+3.8+3+2.2+2.4+1.2)÷7=13÷7=$\frac{13}{7}$万,
答:7天内该风景区平均每天有游客$\frac{13}{7}$万人.
点评 本题考查了正数和负数,利用了有理数的加法运算,总人数除以时间等于平均人数.

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目
14.下列各命题中,是假命题的是( )
| A. | 推论都是定理 | B. | 定理都是命题 | ||
| C. | 命题都是基本事实 | D. | 基本事实都是命题 |
19.某人画二次函数y=ax2+bx+c的图象时,列出下表(计算没有错误):
根据此表判断:一元二次方程ax2+bx+c=0的一个根x1满足下列关系式( )
| X | 3.2 | 3.3 | 3.4 | 3.5 |
| y | -0.56 | -0.17 | 0.08 | 0.44 |
| A. | 3.2<x1<3.3 | B. | 3.3<x1<3.4 | C. | 3.4<x1<3.5 | D. | 3.1<x1<3.2 |
14.x=-2是下列方程( )的解.
| A. | 2x=6 | B. | (x-3)(x+2)=0 | C. | x2=3 | D. | 3x-6=0 |
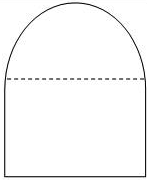 如图,是某一城市地铁的横截面,上面为半圆形,下面为矩形,矩形的长和宽分别为a m与b m.
如图,是某一城市地铁的横截面,上面为半圆形,下面为矩形,矩形的长和宽分别为a m与b m.