题目内容
9.如图①,C地位于A,B两地之间,甲步行直接从C地前往B地,乙骑自行车由C地先回A地,再从A地前往B地(在A地停留时间忽略不计).已知两人同时出发且速度不变,乙的速度是甲的2.5倍,设出发xmin后甲、乙两人离C地的距离分别为y1m,y2m,图②中线段OM表示y1与x的函数图象.(1)甲的速度为80m/min,乙的速度为200m/min;
(2)在图②中画出y2与x的函数图象;
(3)求甲乙两人相遇的时间;
(4)在上述过程中,甲乙两人相距的最远距离为960m.

分析 (1)根据函数图象中点(30,2400),利用“速度=路程÷时间”可算出甲的速度,再根据甲乙速度间的关系可得出乙的速度;
(2)根据乙的速度,以及A、C两地及B、C两地间的距离,利用“时间=路程÷速度”可找出函数图象经过点(0,0)、(3,600)、(6,0)、(18,2400),按照顺序连接两点即可得出结论;
(3)设甲乙两人相遇的时间为xmin,结合(2)y2与x的函数图象可知,乙相当于比甲晚出发6分钟,依照“路程=速度×时间”可列出关于x的一元一次方程,解方程即可得出结论;
(4)结合函数图象可知:最值只有可能出现在两种情况下,乙刚到A地时或乙到B地时,分别求出两种情形下两人间的距离,再作比较即可得出结论.
解答 解:(1)甲的速度为:2400÷30=80(m/min);
乙的速度为:80×2.5=200(m/min).
故答案为:80;200.
(2)600÷200=3(min),
600×2÷200=6(min).
2400÷200+6=18(min).
∴y2与x的函数图象过点(0,0)、(3,600)、(6,0)、(18,2400).
画出图形如图所示.
(3)设甲乙两人相遇的时间为xmin,
依题意得:80x=200(x-6),
解得:x=10.
答:甲乙两人相遇的时间为10min.
(4)∵乙的速度>甲的速度,
∴当x=3时,乙达到A地,此时甲乙两人间距可能最远,
3×(80+200)=840(m);
当x=18时,甲乙两人间距为:
2400-80×18=960(m).
∵960>840,
∴甲乙两人相距的最远距离为960m.
故答案为:960.
点评 本题考查了一次函数的应用以及解一元一次方程,解题的关键是:(1)根据数量关系直接计算;(2)找出拐点坐标;(3)依照数量关系列出关于x的方程;(4)找出极值,再比较极值的大小,确定最值.本题属于中档题,难度不大,解决该题型题目时,根据数量关系列出方程(或方程组)是关键.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 寒假结束了,为了了解九年级学生寒假体育锻炼情况,王老师调查了九年级所有学生寒假体育锻炼时间,并随即抽取10名学生进行统计,制作出如下统计图表:
寒假结束了,为了了解九年级学生寒假体育锻炼情况,王老师调查了九年级所有学生寒假体育锻炼时间,并随即抽取10名学生进行统计,制作出如下统计图表:| 编号 | 成绩 | 编号 | 成绩 |
| ① | B | ⑥ | A |
| ② | A | ⑦ | B |
| ③ | B | ⑧ | C |
| ④ | B | ⑨ | B |
| ⑤ | C | ⑩ | A |
(1)将条形统计图补充完整;
(2)若用扇形统计图来描述10名学生寒假体育锻炼情况,分别求A,B,C三个等级对应的扇形圆心角的度数;
(3)已知这次统计中共有60名学生寒假体育锻炼时间是A等,请你估计这次统计中B等,C等的学生各有多少名?
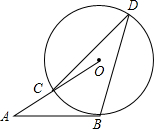 如图,AB是⊙O的切线,切点为B,AO交⊙O于点C,D是优弧BC上一点,∠A=30°,则∠D为( )
如图,AB是⊙O的切线,切点为B,AO交⊙O于点C,D是优弧BC上一点,∠A=30°,则∠D为( )| A. | 25° | B. | 30° | C. | 35° | D. | 45° |




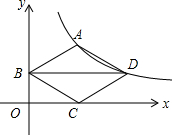 如图,菱形ABCD的对角线BD与x轴平行,点B、C的坐标分别是(0,1)、(2,0),点A、D在函数y=$\frac{k}{x}$(x>0)的图象上,则k的值为4.
如图,菱形ABCD的对角线BD与x轴平行,点B、C的坐标分别是(0,1)、(2,0),点A、D在函数y=$\frac{k}{x}$(x>0)的图象上,则k的值为4.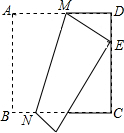 如图,将边长为12cm的正方形纸片ABCD折叠,使得点A落在边CD上的E点,折痕为MN,若MN的长为13cm,则CE的长为7cm.
如图,将边长为12cm的正方形纸片ABCD折叠,使得点A落在边CD上的E点,折痕为MN,若MN的长为13cm,则CE的长为7cm.