题目内容
13.已知函数y=4x2-4ax+a2-2a+2在0≤x≤2上有最小值3,则a的值1-$\sqrt{2}$或5+$\sqrt{10}$.分析 分析函数图象的开口方向和对称轴,进而可分析出函数在0≤x≤2上的增减性,结合函数的最小值为3,分类讨论可求出满足条件的a值.
解答 解:配方得y=4(x-$\frac{a}{2}$)2-2a+2,故函数图象开口朝上,且对称轴为x=$\frac{a}{2}$.
当$\frac{a}{2}$≤0,即a≤0时,当x=0时,y最小值=a2-2a+2=3,解得a=1-$\sqrt{2}$或a=1+$\sqrt{2}$(舍);
当0<$\frac{a}{2}$<2,即0<a<4时,当x=$\frac{a}{2}$时,y最小值=-2a+2=3,解得a=-$\frac{1}{2}$(舍);
当$\frac{a}{2}$≥2时,当x=2时,y最小值=8-8a+a2-2a+2=3,
解得a=5+$\sqrt{10}$.
综上所述,a的值是1-$\sqrt{2}$或5+$\sqrt{10}$.
故答案是:1-$\sqrt{2}$或5+$\sqrt{10}$.
点评 本题考查的知识点是二次函数在定区间上的最值问题,熟练掌握二次函数的图象和性质是解答的关键.

练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目
 如图,在△ABC中,AB=6,AC=8,∠CAB=60°.求△ABC的内切圆⊙I的半径和外接圆⊙O的半径.
如图,在△ABC中,AB=6,AC=8,∠CAB=60°.求△ABC的内切圆⊙I的半径和外接圆⊙O的半径. 如图,△ABC所在的平面上,满足△BCP与△ABC全等的点P共有9个.
如图,△ABC所在的平面上,满足△BCP与△ABC全等的点P共有9个.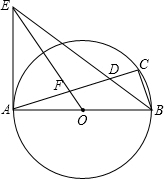 如图,AB为⊙O的直径,点C在⊙O上,∠ABC的平分线与AC相交于点D,与⊙O过点A的切线相交于点E,连接OE交AC于F.
如图,AB为⊙O的直径,点C在⊙O上,∠ABC的平分线与AC相交于点D,与⊙O过点A的切线相交于点E,连接OE交AC于F.