题目内容
 如图,AE⊥AB,BF⊥AB,AB的中垂线交AB于N,交EF于M,求证:MN=
如图,AE⊥AB,BF⊥AB,AB的中垂线交AB于N,交EF于M,求证:MN=| 1 |
| 2 |
考点:三角形中位线定理,全等三角形的判定与性质,线段垂直平分线的性质
专题:证明题
分析:连接BE,延长MN交BE于点C,根据已知条件求出和三角形中位线定理得出MC=
BF,NC=
AE,再根据MN=MC-NC,即可得出答案.
| 1 |
| 2 |
| 1 |
| 2 |
解答:
 解:连接BE,延长MN交BE于点C,
解:连接BE,延长MN交BE于点C,
∵AE⊥AB,BF⊥AB,MN⊥AB,
∴MC=
BF,NC=
AE,
∵MN=MC-NC,
∴MN=
BF-
AE=
(BF-AE).
 解:连接BE,延长MN交BE于点C,
解:连接BE,延长MN交BE于点C,∵AE⊥AB,BF⊥AB,MN⊥AB,
∴MC=
| 1 |
| 2 |
| 1 |
| 2 |
∵MN=MC-NC,
∴MN=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
点评:此题考查了三角形中位线定理,根据题意作出辅助线,运用三角形的中位线等于三角形底边的一半是本题的关键.

练习册系列答案
相关题目
在直角坐标系中,一直线l向下平移3个单位后所得直线b经过点A(0,3),将直线b绕点A顺时针旋转60°后所得直线经过点B(-
,0),则直线l的函数关系式为( )
| 3 |
A、y=-
| ||||
B、y=-
| ||||
C、y=-
| ||||
D、y=-
|
 如图,边长为a的正六边形内有两个三角形(数据如图),则
如图,边长为a的正六边形内有两个三角形(数据如图),则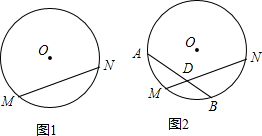 如图1,已知⊙O的弦MN所对的弧是120°,圆心O到MN所在的直线的距离是4.
如图1,已知⊙O的弦MN所对的弧是120°,圆心O到MN所在的直线的距离是4.
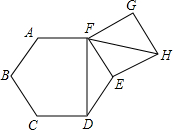 如图,在正六边形ABCDEF的外侧,作正方形EFGH,则∠DFH的度数为
如图,在正六边形ABCDEF的外侧,作正方形EFGH,则∠DFH的度数为 如图,∠AOB=110°,则∠ACB=
如图,∠AOB=110°,则∠ACB=