题目内容
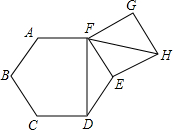如图，在正六边形ABCDEF的外侧，作正方形EFGH，则∠DFH的度数为考点：多边形内角与外角
专题：
分析：△EFH是等腰直角三角形，可求∠EFH的度数，△DEF是等腰三角形，只要求出顶角∠DEF的度数就可以求出∠EFD的度数，再把两个角的度数相加即可求解．
解答：
解：观察图形可知，
△EFH是等腰直角三角形，
则∠EFH=45°，
△DEF是等腰三角形，
∵∠DEF=120°，
∴∠EFD=（180°-120°）÷2=30°，
∴∠DFH=45°+30°=75°．
故答案为：75°．
△EFH是等腰直角三角形，
则∠EFH=45°，
△DEF是等腰三角形，
∵∠DEF=120°，
∴∠EFD=（180°-120°）÷2=30°，
∴∠DFH=45°+30°=75°．
故答案为：75°．
点评：考查了多边形内角与外角，本题就是一个求正多边形的内角的问题，注意到△EFH是等腰直角三角形，△DEF是等腰三角形是解决本题的关键．
练习册系列答案
优加精卷系列答案
相关题目
某车间周内计划每天生产100辆电动车，由于工人实行轮休，每天上班人数不一定相等，实际每天生产量与计划量相比情况如下表（增加的车辆数为正数，减少的车辆数为负数）
如图，AE⊥AB，BF⊥AB，AB的中垂线交AB于N，交EF于M，求证：MN=
如图，点D在以AC为直径的⊙O上，若∠BDC=35°，那么∠ACB的度数是（ ）| A、35° | B、55° |
| C、70° | D、110° |
下列各几何体均由三个大小相同的正方体组成，其中正视图为右图的是（ ）A、 |
B、 |
C、 |
D、 |
如图，△ABC中，∠A=90°，点D、E分别在AC和AB上，试说明BD2-DE2=BC2-CE2．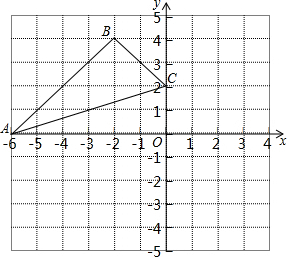
如图，在直角坐标系中，△ABC三个顶点的坐标分别为A（-6，0），B（-2，4），C（0，2）．分别以点C，O为位似中心，画出△ABC的位似图形△CDE和△FGH，且同时满足下列两个条件：