题目内容
 如图,∠AOB=110°,则∠ACB=
如图,∠AOB=110°,则∠ACB=考点:圆周角定理
专题:
分析:首先在⊙O上取点D,连接AD,BD,由∠AOB=110°,即可求得∠D的度数,再由圆的内接四边形的性质,求得∠ACB的度数.
解答:
 解:在⊙O上取点D,连接AD,BD,
解:在⊙O上取点D,连接AD,BD,
∵∠AOB=110°,
∴∠D=
∠AOB=55°,
∴∠ACB=180°-∠AOB=125°.
故答案为:125°.
 解:在⊙O上取点D,连接AD,BD,
解:在⊙O上取点D,连接AD,BD,∵∠AOB=110°,
∴∠D=
| 1 |
| 2 |
∴∠ACB=180°-∠AOB=125°.
故答案为:125°.
点评:此题考查了圆周角定理以及圆的内接四边形的性质.此题比较简单,注意掌握辅助线的作法,注意掌握数形结合思想的应用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 下列各几何体均由三个大小相同的正方体组成,其中正视图为右图的是( )
下列各几何体均由三个大小相同的正方体组成,其中正视图为右图的是( )A、 |
B、 |
C、 |
D、 |
下列计算正确的是( )
| A、a3•a=a3 |
| B、(2a+b)2=4a2+b2 |
| C、a8b÷a2=a4b |
| D、(-3ab3)2=9a2b6 |
不改变分式
的值,把它的分子和分母中的各项都化为整数,则所得的结果为( )
| 0.3x-1 | ||
x+
|
A、
| ||
B、
| ||
C、
| ||
D、
|
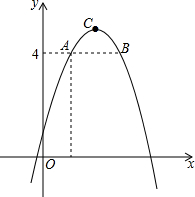 如图,二次函数y=ax2-4ax+b的图象过点A(1,4),B(x,4),该函数图象的顶点为C,且S△ABC=1,求二次函数的解析式.
如图,二次函数y=ax2-4ax+b的图象过点A(1,4),B(x,4),该函数图象的顶点为C,且S△ABC=1,求二次函数的解析式. 如图,AE⊥AB,BF⊥AB,AB的中垂线交AB于N,交EF于M,求证:MN=
如图,AE⊥AB,BF⊥AB,AB的中垂线交AB于N,交EF于M,求证:MN= 如图,△ABC中,∠A=90°,点D、E分别在AC和AB上,试说明BD2-DE2=BC2-CE2.
如图,△ABC中,∠A=90°,点D、E分别在AC和AB上,试说明BD2-DE2=BC2-CE2.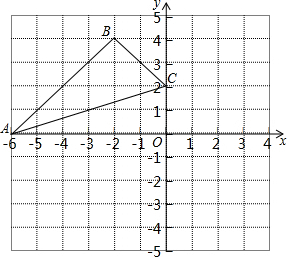 如图,在直角坐标系中,△ABC三个顶点的坐标分别为A(-6,0),B(-2,4),C(0,2).分别以点C,O为位似中心,画出△ABC的位似图形△CDE和△FGH,且同时满足下列两个条件:
如图,在直角坐标系中,△ABC三个顶点的坐标分别为A(-6,0),B(-2,4),C(0,2).分别以点C,O为位似中心,画出△ABC的位似图形△CDE和△FGH,且同时满足下列两个条件: