题目内容
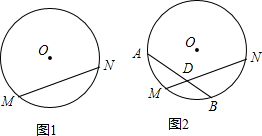 如图1,已知⊙O的弦MN所对的弧是120°,圆心O到MN所在的直线的距离是4.
如图1,已知⊙O的弦MN所对的弧是120°,圆心O到MN所在的直线的距离是4.(1)求弦MN的长;
(2)如图2,若点M是
 |
| AB |
考点:垂径定理,勾股定理,圆周角定理
专题:
分析:(1)连接OM、ON,过O作OD⊥MN于D,根据垂径定理求出MN=2MD,根据等腰三角形的性质求出∠MOD=60°,求出∠OMD,解直角三角形求出即可;
(2)连接BN,求出
和
的度数相等,设度数为x°,根据劣弧MN的度数是120°,求出优弧MN的度数为240°,根据三角形外角性质得出∠ADN=∠ABN+∠MNB,即可求出答案.
(2)连接BN,求出
 |
| AM |
 |
| BM |
解答:
解:(1)如图:连接OM、ON,过O作OD⊥MN于D,
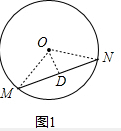
∵⊙O的弦MN所对的弧是120°,
∴∠MON=120°,
∵OM=ON,
∴∠MOD=∠NOD=60°,MN=2MD,
∴∠OMD=30°,
∵圆心O到MN所在的直线的距离是4,
∴OD=4,
∴OM=2OD=8,由勾股定理得:MD=
=4
,
∴MN=2MD=8
;
(2)如图:连接BN,
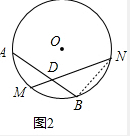
∵点M是
的中点,
∴
和
的度数相等,设度数为x°,
∵劣弧MN的度数是120°,
∴优弧MN的度数为360°-120°=240°,
∵∠ADN=∠ABN+∠MNB=
(240°-x°)+
•x°=120°.
故答案为:120.

∵⊙O的弦MN所对的弧是120°,
∴∠MON=120°,
∵OM=ON,
∴∠MOD=∠NOD=60°,MN=2MD,
∴∠OMD=30°,
∵圆心O到MN所在的直线的距离是4,
∴OD=4,
∴OM=2OD=8,由勾股定理得:MD=
| 82-42 |
| 3 |
∴MN=2MD=8
| 3 |
(2)如图:连接BN,

∵点M是
 |
| AB |
∴
 |
| AM |
 |
| BM |
∵劣弧MN的度数是120°,
∴优弧MN的度数为360°-120°=240°,
∵∠ADN=∠ABN+∠MNB=
| 1 |
| 2 |
| 1 |
| 2 |
故答案为:120.
点评:本题考查了垂径定理,勾股定理,含30度角的直角三角形的性质,圆周角定理的应用,综合运用性质进行推理和计算是解此题的关键,注意:圆心角的度数等于它所对的弧的度数.

练习册系列答案
 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目
已知△ABC,D,E,F分别是AB,BC,CA的中点,设
=
,
=
,则
+
是( )
| AB |
| a |
| AC |
| b |
| DE |
| DF |
A、
| ||||||
B、-
| ||||||
C、
| ||||||
D、
|
 如图:⊙O1和⊙O2是等圆,外切于点A,过点A的直线交⊙O1于B点,交⊙O2于点C,求证:AB=AC.
如图:⊙O1和⊙O2是等圆,外切于点A,过点A的直线交⊙O1于B点,交⊙O2于点C,求证:AB=AC. 某车间周内计划每天生产100辆电动车,由于工人实行轮休,每天上班人数不一定相等,实际每天生产量与计划量相比情况如下表(增加的车辆数为正数,减少的车辆数为负数)
某车间周内计划每天生产100辆电动车,由于工人实行轮休,每天上班人数不一定相等,实际每天生产量与计划量相比情况如下表(增加的车辆数为正数,减少的车辆数为负数)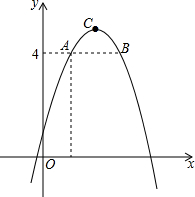 如图,二次函数y=ax2-4ax+b的图象过点A(1,4),B(x,4),该函数图象的顶点为C,且S△ABC=1,求二次函数的解析式.
如图,二次函数y=ax2-4ax+b的图象过点A(1,4),B(x,4),该函数图象的顶点为C,且S△ABC=1,求二次函数的解析式. 如图,AE⊥AB,BF⊥AB,AB的中垂线交AB于N,交EF于M,求证:MN=
如图,AE⊥AB,BF⊥AB,AB的中垂线交AB于N,交EF于M,求证:MN= 如图,在直角坐标系中,△ABC三个顶点的坐标分别为A(-6,0),B(-2,4),C(0,2).分别以点C,O为位似中心,画出△ABC的位似图形△CDE和△FGH,且同时满足下列两个条件:
如图,在直角坐标系中,△ABC三个顶点的坐标分别为A(-6,0),B(-2,4),C(0,2).分别以点C,O为位似中心,画出△ABC的位似图形△CDE和△FGH,且同时满足下列两个条件: