��Ŀ����
12��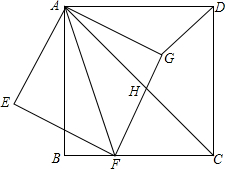 ��ͼ��������ABCD�У���F��BC����һ�㣬����AF����AFΪ�Խ�����������AEFG����FG��������ABCD�ĶԽ���AC�ཻ�ڵ�H������DG��
��ͼ��������ABCD�У���F��BC����һ�㣬����AF����AFΪ�Խ�����������AEFG����FG��������ABCD�ĶԽ���AC�ཻ�ڵ�H������DG����1����գ�����BAF=18�㣬���DAG=27�㣻
��2��������F���߶�BC���˶�ʱ������B��C�����غϣ�����FC=x��DG=y������y��x֮��ĺ�����ϵʽ��
��3����$\frac{BF}{FC}$=$\frac{1}{2}$�������$\frac{FC}{FH}$��ֵ��
���� ��1�����ı���ABCD��AEFG�������Σ��õ���BAC=��GAF=45�㣬���ǵõ���BAF+��FAC=��FAC+��GAC=45�㣬�Ƴ���HAG=��BAF=18�㣬���ڡ�DAG+��GAH=��DAC=45�㣬���ǵõ����ۣ�
��2�����ı���ABCD��AEFG�������Σ��Ƴ�$\frac{AD}{AC}=\frac{\sqrt{2}}{2}$��$\frac{AG}{AF}$=$\frac{\sqrt{2}}{2}$���õ�$\frac{AD}{AC}=\frac{AG}{AF}$�����ڡ�DAG=��CAF���õ���ADG�ס�CAF���б���ʽ���ɵõ������
��3����BF=k��CF=2k����AB=BC=3k�����ݹ��ɶ����õ�AF=$\sqrt{A{B}^{2}+B{F}^{2}}$=$\sqrt{��3k��^{2}+{k}^{2}}$=$\sqrt{10}$k��AC=$\sqrt{2}$AB=3$\sqrt{2}$k�����ڡ�AFH=��ACF����FAH=��CAF�����ǵõ���AFH�ס�ACF���õ�����ʽ���ɵõ����ۣ�
��� �⣺��1�����ı���ABCD��AEFG�������Σ�
���BAC=��GAF=45�㣬
���BAF+��FAC=��FAC+��GAC=45�㣬
���HAG=��BAF=18�㣬
�ߡ�DAG+��GAH=��DAC=45�㣬
���DAG=45��-18��=27�㣬
�ʴ�Ϊ��27��
��2�����ı���ABCD��AEFG�������Σ�
��$\frac{AD}{AC}=\frac{\sqrt{2}}{2}$��$\frac{AG}{AF}$=$\frac{\sqrt{2}}{2}$��
��$\frac{AD}{AC}=\frac{AG}{AF}$��
�ߡ�DAG+��GAC=��FAC+��GAC=45�㣬
���DAG=��CAF��
���ADG�ס�CAF��
��$\frac{DG}{CF}=\frac{AD}{AC}=\frac{\sqrt{2}}{2}$��
����$\frac{y}{x}=\frac{\sqrt{2}}{2}$��
��y=$\frac{\sqrt{2}x}{2}$��
��3����$\frac{BF}{FC}$=$\frac{1}{2}$��
��BF=k��CF=2k����AB=BC=3k��
��AF=$\sqrt{A{B}^{2}+B{F}^{2}}$=$\sqrt{��3k��^{2}+{k}^{2}}$=$\sqrt{10}$k��AC=$\sqrt{2}$AB=3$\sqrt{2}$k��
���ı���ABCD��AEFG�������Σ�
���AFH=��ACF����FAH=��CAF��
���AFH�ס�ACF��
��$\frac{AF}{AC}=\frac{FH}{CF}$��
����$\frac{\sqrt{10}k}{3\sqrt{2}k}=\frac{FH}{2K}$��
��FH=$\frac{2\sqrt{5}}{3}$k��
��$\frac{CF}{FH}$=$\frac{2k}{\frac{2\sqrt{5}k}{3}}$=$\frac{3\sqrt{5}}{5}$��
���� ���⿼���������ε����ʣ����������ε��ж������ʣ����ɶ������������������ǽ���Ĺؼ���

| A�� | ��-1��1�� | B�� | ��-1��5�� | C�� | ��3��1�� | D�� | ��3��-5�� |
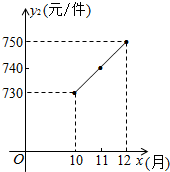 ij��ҵΪ����������ҵ�����ṩ�������������Ԫ�ߵ͵�Ӱ�죬��ȥ��1��9�£��������ԭ���ϼ۸�һ·������ÿ�������ԭ���ϼ۸�y1��Ԫ�����·�x��1��x��9����xȡ������֮��ĺ�����ϵ���±���
ij��ҵΪ����������ҵ�����ṩ�������������Ԫ�ߵ͵�Ӱ�죬��ȥ��1��9�£��������ԭ���ϼ۸�һ·������ÿ�������ԭ���ϼ۸�y1��Ԫ�����·�x��1��x��9����xȡ������֮��ĺ�����ϵ���±���| �·�x | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| �۸�y1��Ԫ/���� | 560 | 580 | 600 | 620 | 640 | 660 | 680 | 700 | 720 |
��1����۲����еı�������ѧ����һ�κ�������������������κ������й�֪ʶ��ֱ��д��y1��x֮��ĺ�����ϵʽ��������ͼ��ʾ�ı仯���ƣ�ֱ��д��y2��x֮�������һ�κ�����ϵʽ��
��2����ȥ������ÿ�����ۼ�Ϊ1000Ԫ������ÿ������������ɱ�Ϊ50Ԫ�������ɱ�30Ԫ���������1��9�µ�������p1����������·�x���㺯����ϵʽp=0.1x+1.1��1��x��9����xȡ������10��12�µ�������p2����������·�x���㺯����ϵʽp2=-0.1x+2.9��10��x��12����xȡ����������ȥ���ĸ������۸��������������������������
��3������1��5�£�ÿ�������ԭ���ϼ۸����ȥ��12������60Ԫ�������ɱ���ȥ������20%�������ɱ�û�б仯������ҵ��ÿ��������ۼ���ȥ��Ļ��������a%�����ͬʱÿ������������ȥ��12�µĻ����ϼ���0.1a%���������ڱ�֤ÿ����������������ǰ���£������1��5�µ�������1700��Ԫ����������ο��������ݣ������a������ֵ��
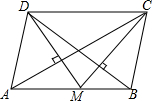 ��M��ƽ���ı���ABCD�ı�AB�ϣ�����AM��MB=4��3����DM��CM�ֱ�ֱ��AC��BD����BC=5cm������?ABCD������Ƕ���cm2��
��M��ƽ���ı���ABCD�ı�AB�ϣ�����AM��MB=4��3����DM��CM�ֱ�ֱ��AC��BD����BC=5cm������?ABCD������Ƕ���cm2��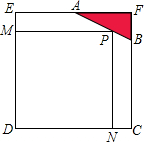 ��֪�߳�Ϊ4�������ν�ȡһ���Ǻ��Ϊ�����ABCDE����ͼ��������AF=2��BF=1������AB����һ��Pʹ����MPND�����������������ʱ����MPND�ı߳�DN��PN��
��֪�߳�Ϊ4�������ν�ȡһ���Ǻ��Ϊ�����ABCDE����ͼ��������AF=2��BF=1������AB����һ��Pʹ����MPND�����������������ʱ����MPND�ı߳�DN��PN�� ��ͼ��C����ABΪֱ���ġ�O��һ�㣬��O��OE��AC�ڵ�E������A����O�����߽�OE���ӳ����ڵ�F������CF���ӳ���BA���ӳ����ڵ�P��
��ͼ��C����ABΪֱ���ġ�O��һ�㣬��O��OE��AC�ڵ�E������A����O�����߽�OE���ӳ����ڵ�F������CF���ӳ���BA���ӳ����ڵ�P��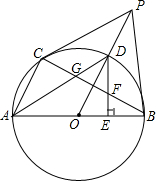 ��ͼ��ABΪ��O��ֱ����PBΪ��O�����ߣ�AC��OP����C�ڡ�O�ϣ�OP����O��D��DA��BC��G��
��ͼ��ABΪ��O��ֱ����PBΪ��O�����ߣ�AC��OP����C�ڡ�O�ϣ�OP����O��D��DA��BC��G��