题目内容
9. 如图,用宽度都是2的矩形纸带叠放成一个锐角为60°的四边形,则此四边形的面积S为( )
如图,用宽度都是2的矩形纸带叠放成一个锐角为60°的四边形,则此四边形的面积S为( )| A. | 4 | B. | $\frac{4}{3}$$\sqrt{3}$ | C. | $\frac{2}{3}$$\sqrt{3}$ | D. | $\frac{8}{3}$$\sqrt{3}$ |
分析 先根据两组对边分别平行证明四边形ABCD是平行四边形,再根据两张纸条的宽度相等,利用面积求出AB=BC,然后根据邻边相等的平行四边形是菱形即可证明;根据宽度是2与∠DAB=60°求出菱形的边长,然后利用菱形的面积=底×高计算即可.
解答 解:纸条的对边平行,即AB∥CD,AD∥BC,
∴四边形ABCD是平行四边形,
∵两张纸条的宽度都是2cm,
∴S四边形ABCD=AB×2=BC×2,
∴AB=BC,
∴平行四边形ABCD是菱形,
即四边形ABCD是菱形;
如图:
过A作DE⊥AB,垂足为E,
∵∠DAB=60°,
∴∠ADE=90°-60°=30°,
∴AD=2AE,
在△ADE中,AD2=DE2+AE2,
即AD2=$\frac{1}{4}$AD2+22,
∴AD=$\frac{4}{3}$$\sqrt{3}$,
∴S四边形ABCD=AB•DE=$\frac{4}{3}$$\sqrt{3}$×2=$\frac{8}{3}$$\sqrt{3}$.
故选:D.
点评 本题考查了菱形的判定与性质,根据宽度相等,利用面积法求出边长相等是证明菱形的关键.

练习册系列答案
相关题目
9.已知xa=3,xb=5,则x2a+b=( )
| A. | 45 | B. | 50 | C. | $\frac{6}{5}$ | D. | 11 |
 如图,C是以AB为直径的⊙O上一点,过O作OE⊥AC于点E,过点A作⊙O的切线交OE的延长线于点F,连接CF并延长交BA的延长线于点P.
如图,C是以AB为直径的⊙O上一点,过O作OE⊥AC于点E,过点A作⊙O的切线交OE的延长线于点F,连接CF并延长交BA的延长线于点P.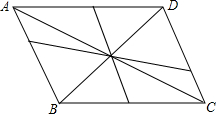 如图,直线BD可以将平行四边形ABCD分成全等的两部分,这样的直线还有很多.
如图,直线BD可以将平行四边形ABCD分成全等的两部分,这样的直线还有很多.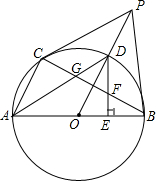 如图,AB为⊙O的直径,PB为⊙O的切线,AC∥OP,点C在⊙O上,OP交⊙O于D,DA交BC于G.
如图,AB为⊙O的直径,PB为⊙O的切线,AC∥OP,点C在⊙O上,OP交⊙O于D,DA交BC于G.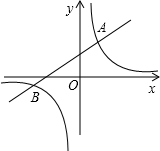 如图,已知反比例函数y=$\frac{k}{x}$与一次函数y=x+b的图象在第一象限相交于点A(1,-k+4)
如图,已知反比例函数y=$\frac{k}{x}$与一次函数y=x+b的图象在第一象限相交于点A(1,-k+4)