题目内容
2.化简:(1)$\sqrt{120}$;
(2)$\sqrt{200}$;
(3)$\sqrt{8{x}^{3}y}$(x≥0,y≥0);
(4)$\sqrt{12{x}^{3}{y}^{5}}$(x≥0,y≥0).
分析 (1)$\sqrt{120}=\sqrt{4×30}$,然后将4开到根号外即可;
(2)$\sqrt{200}=\sqrt{2×100}$,然后100开到根号外即可;
(3)$\sqrt{8{x}^{3}y}=\sqrt{4{x}^{2}•2xy}$,然后将4x2开到根号外即可;
(4)$\sqrt{12{x}^{3}{y}^{5}}=\sqrt{4{x}^{2}{y}^{4}•3xy}$,然后4x2y4开到根号外即可.
解答 解:(1)$\sqrt{120}=\sqrt{4×30}=2\sqrt{30}$;
(2)$\sqrt{200}=\sqrt{2×100}$=10$\sqrt{2}$;
(3)$\sqrt{8{x}^{3}y}=\sqrt{4{x}^{2}•2xy}$=2x$\sqrt{2xy}$;
(4)$\sqrt{12{x}^{3}{y}^{5}}=\sqrt{4{x}^{2}{y}^{4}•3xy}$=$2x{y}^{2}\sqrt{3xy}$.
点评 本题主要考查的是二次根式的化简,化简二次根式的过程,一般按以下步骤:把根号下的带分数或绝对值大于1的小数化成假分数,把绝对值小于1的小数化成分数;被开方数是多项式的要因式分解;使被开方数不含分母;将被开方数中能开的尽方的因数或因式用它的算术平方根代替后移到根号外面;化去分母中的根号;约分.

练习册系列答案
相关题目
2.下列计算正确的是( )
| A. | a3+a4=a7 | B. | a3•a3•a3=3a3 | C. | 3a4•2a3=6a7 | D. | (-a3)4=a7 |
3.下列说法中不正确的是( )
| A. | 平行四边形是中心对称图形 | |
| B. | 斜边及一锐角分别相等的两直角三角形全等 | |
| C. | 两个锐角分别相等的两直角三角形全等 | |
| D. | 一直角边及斜边分别相等的两直角三角形全等 |
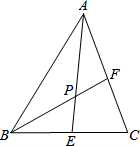 △ABC中,∠ABC=60°,AE、BF是角平分线,且AE、BF交于点P,若AB=6,AP=3PE,则AC长为$\frac{21}{4}$.
△ABC中,∠ABC=60°,AE、BF是角平分线,且AE、BF交于点P,若AB=6,AP=3PE,则AC长为$\frac{21}{4}$.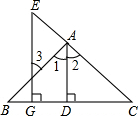 如图,已知AD⊥BC于D,EG⊥BC于G,且∠E=∠3,试说明AD平分∠BAC.
如图,已知AD⊥BC于D,EG⊥BC于G,且∠E=∠3,试说明AD平分∠BAC.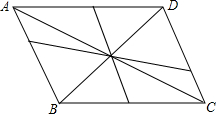 如图,直线BD可以将平行四边形ABCD分成全等的两部分,这样的直线还有很多.
如图,直线BD可以将平行四边形ABCD分成全等的两部分,这样的直线还有很多.