题目内容
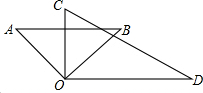 如图,将一副三角板的直角顶点重合,摆放在桌面上.
如图,将一副三角板的直角顶点重合,摆放在桌面上.(1)若∠AOD=140°,则∠BOC=
(2)若∠BOC=30°,则∠AOD=
(3)通过(1)(2)两题的计算,你发现∠AOD与∠BOC有什么数量关系?并说明你的结论.
考点:余角和补角
专题:
分析:(1)从图可以看出,∠BOC的度数正好是两直角相加减去∠AOD的度数,从而问题可解;
(2)从如图可以看出,∠AOD的度数正好是两直角相加减去∠BOC的度数,从而问题可解;
(3)根据直角三角板可得∠AOB=90°,∠COD=90°,然后再根据∠AOD=∠AOB+∠BOD可得∠AOD+∠COB=∠AOB+∠BOD+∠COB=∠AOB+∠COD,进而得到互补.
(2)从如图可以看出,∠AOD的度数正好是两直角相加减去∠BOC的度数,从而问题可解;
(3)根据直角三角板可得∠AOB=90°,∠COD=90°,然后再根据∠AOD=∠AOB+∠BOD可得∠AOD+∠COB=∠AOB+∠BOD+∠COB=∠AOB+∠COD,进而得到互补.
解答:解:(1)∵∠AOB=∠COD=90°,∠AOD=140°
∴∠BOC=∠AOB+∠COD-∠AOD=90°+90°-140°=40°.
故答案为:40°;
(2))∵∠AOB=∠COD=90°,∠BOC=30°
∴∠AOD=∠AOB+∠COD-∠BOC=90°+90°-30°=150°.
故答案为:150°;
(3)∠AOD与∠BOC互补,即∠AOD+∠BOC=180°.
理由如下:
∵∠AOB=90°,∠COD=90°,
∴∠AOD+∠COB=∠AOB+∠BOD+∠COB=∠AOB+∠COD=180°.
∴∠AOD与∠BOC互补.
∴∠BOC=∠AOB+∠COD-∠AOD=90°+90°-140°=40°.
故答案为:40°;
(2))∵∠AOB=∠COD=90°,∠BOC=30°
∴∠AOD=∠AOB+∠COD-∠BOC=90°+90°-30°=150°.
故答案为:150°;
(3)∠AOD与∠BOC互补,即∠AOD+∠BOC=180°.
理由如下:
∵∠AOB=90°,∠COD=90°,
∴∠AOD+∠COB=∠AOB+∠BOD+∠COB=∠AOB+∠COD=180°.
∴∠AOD与∠BOC互补.
点评:此题主要考查学生对角的计算的理解和掌握,解答此题的关键是让学生通过观察图示,发现几个角之间的关系.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
 如图,数轴上点A表示
如图,数轴上点A表示 如图,已知直线AB和CD相交于点O,∠COE=90°,OF平分∠AOE.
如图,已知直线AB和CD相交于点O,∠COE=90°,OF平分∠AOE. 如图,AB,AD,DC与半圆O均相切,AD∥BC,AB=8,CD=5,则BC=
如图,AB,AD,DC与半圆O均相切,AD∥BC,AB=8,CD=5,则BC=