题目内容
9.已知在Rt△ABC中,∠C=90°,如果BC=2,∠A=α,则AC的长为( )| A. | 2sinα | B. | 2cosα | C. | 2tanα | D. | 2cotα |
分析 根据锐角三角函数的定义得出cotA=$\frac{AC}{BC}$,代入求出即可.
解答 解:∵在Rt△ABC中,∠C=90°,
∴cotA=$\frac{AC}{BC}$,
∵BC=2,∠A=α,
∴AC=2cotα,
故选D.
点评 本题考查了锐角三角函数的定义,能熟记锐角三角函数的定义是解此题的关键,注意:在Rt△ACB中,∠ACB=90°,则sinA=$\frac{BC}{AB}$,cosA=$\frac{AC}{AB}$,tanA=$\frac{BC}{AC}$,cotA=$\frac{AC}{BC}$.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
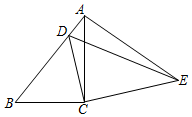 如图,在△ABC中,∠ACB=90°,AB=9,cosB=$\frac{2}{3}$,把△ABC绕着点C旋转,使点B与AB边上的点D重合,点A落在点E,则点A、E之间的距离为4$\sqrt{5}$.
如图,在△ABC中,∠ACB=90°,AB=9,cosB=$\frac{2}{3}$,把△ABC绕着点C旋转,使点B与AB边上的点D重合,点A落在点E,则点A、E之间的距离为4$\sqrt{5}$. 如图,在平面直角坐标系xOy中,抛物线y=ax2+bx+4与x轴的正半轴相交于点A,与y轴相交于点B,点C在线段OA上,点D在此抛物线上,CD⊥x轴,且∠DCB=∠DAB,AB与CD相交于点E.
如图,在平面直角坐标系xOy中,抛物线y=ax2+bx+4与x轴的正半轴相交于点A,与y轴相交于点B,点C在线段OA上,点D在此抛物线上,CD⊥x轴,且∠DCB=∠DAB,AB与CD相交于点E.