题目内容
4.计算:2sin60°-|cot30°-cot45°|+$\frac{tan45°}{cos30°-1}$.分析 首先根据特殊角的三角函数进行代入,然后再根据绝对值的性质计算绝对值,然后合并同类二次根式即可.
解答 解:原式=2×$\frac{\sqrt{3}}{2}$-|$\sqrt{3}-$1|+$\frac{1}{\frac{\sqrt{3}}{2}-1}$,
=$\sqrt{3}$$-\sqrt{3}$+1+$\frac{2}{\sqrt{3}-2}$,
=-2$\sqrt{3}$-3.
点评 此题主要考查了实数运算,正确记忆特殊角的三角函数值是解题关键.

练习册系列答案
相关题目
12.如果将某一抛物线向右平移2个单位,再向上平移2各单位后所得新抛物线的表达式是y=2(x-1)2,那么原抛物线的表达式是( )
| A. | y=2(x-3)2-2 | B. | y=2(x-3)2+2 | C. | y=2(x+1)2-2 | D. | y=2(x+1)2+2 |
9.已知在Rt△ABC中,∠C=90°,如果BC=2,∠A=α,则AC的长为( )
| A. | 2sinα | B. | 2cosα | C. | 2tanα | D. | 2cotα |
 已知:如图,梯形ABCD中,AD∥BC,∠ABD=∠C,AD=4,BC=9,锐角∠DBC的正弦值为$\frac{2}{3}$.
已知:如图,梯形ABCD中,AD∥BC,∠ABD=∠C,AD=4,BC=9,锐角∠DBC的正弦值为$\frac{2}{3}$.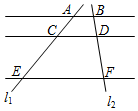 如图,已知AB∥CD∥EF,它们依次交直线l1、l2于点A、C、E和点B、D、F,如果AC:CE=3:5,BF=9,那么DF=$\frac{45}{8}$.
如图,已知AB∥CD∥EF,它们依次交直线l1、l2于点A、C、E和点B、D、F,如果AC:CE=3:5,BF=9,那么DF=$\frac{45}{8}$.