题目内容
7.若函数y=a(x-h)2+k的图象经过原点,最小值为8且形状与抛物线y=-2x2-2x+3相同,则此函数关系式y=-2x2+8x或y=-2x2-8x.分析 函数图象经过原点,可得等式ah2+k=0;已知最小值8,可得k=8;根据抛物线形状相同可知a=-2,从而可求h.
解答 解:∵函数y=a(x-h)2+k的图象经过原点,把(0,0)代入解析式,得:ah2+k=0,
∵最小值为8,即函数的开口向下,a<0,顶点的纵坐标k=8,
又∵形状与抛物线y=-2x2-2x+3相同,
∴二次项系数a=-2,
把a=-2,k=8代入ah2+k=0中,得h=±2,
∴函数解析式是:y=-2(x-2)2+8或y=-2(x+2)2+8,
即:y=-2x2+8x或y=-2x2-8x.
故答案为y=-2x2+8x或y=-2x2-8x.
点评 此题考查了待定系数法求二次函数解析式,熟练掌握待定系数法是解本题的关键.

练习册系列答案
 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
2.体育测试时,一名九年级的学生推铅球,已知铅球所经过的路线为抛物线y=-$\frac{1}{12}$x2+x+$\frac{7}{3}$(单位:米)的一部分,根据关系式回答,该同学的成绩是( )
| A. | $\frac{7}{3}$米 | B. | $\frac{16}{3}$米 | C. | 14米 | D. | 6米 |
19.对于函数y=-$\frac{6}{x}$,下列说法错误的是( )
| A. | 它的图象分布在第二、四象限 | B. | 它的图象与直线y=x无交点 | ||
| C. | 当x>0时,y的值随x的增大而增大 | D. | 当x<0时,y的值随x的增大而减小 |
17.下列计算正确的是( )
| A. | a+a2=a3 | B. | 2a+5a=7a | C. | (a2)3=a5 | D. | a8÷a4=a2 |
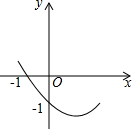 如图所示,已知二次函数y=ax2+bx+c的图象经过(-1,0)和(0,-1)两点,则化简代数式$\sqrt{(a-\frac{1}{a})^{2}+4}$+$\sqrt{(a+\frac{1}{a})^{2}-4}$=$\frac{2}{a}$.
如图所示,已知二次函数y=ax2+bx+c的图象经过(-1,0)和(0,-1)两点,则化简代数式$\sqrt{(a-\frac{1}{a})^{2}+4}$+$\sqrt{(a+\frac{1}{a})^{2}-4}$=$\frac{2}{a}$.
 如图,O为直线AB上一点,且∠BOC=3∠AOC,OC平分∠AOD.
如图,O为直线AB上一点,且∠BOC=3∠AOC,OC平分∠AOD.