Question

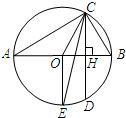如图，AB为⊙O的直径，CD为弦，且CD⊥AB，垂足为H，⊙O的半径为1，CD=

3

，圆周上到直线AC距离为

1

2

的点有多少个？并说明理由．

Answer 1

考点：垂径定理,三角形中位线定理

专题：计算题

分析：作OM⊥AC于M，交⊙O于F，如图，根据垂径定理由AB⊥CD得CH=

1

2

CD=

3

2

，在Rt△OCH中利用勾股定理计算出OH=

1

2

，则OH=BH，根据等腰三角形的判定得CB=CO=1，再由OM⊥AC得到AM=CM，则OM为△ABC的中位线，根据三角形中位线性质得OM=

1

2

BC=

1

2

，所以FM=OF-OM=

1

2

，于是得到在弧AC上点AC的距离为1的点有一个，加上在优弧AEC上到AC的距离为

1

2

的点一定有两个，所以圆周上存在3个点到直线AC的距离为

1

2

．

解答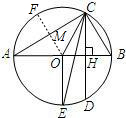：解：圆周上存在3个点到直线AC的距离为

1

2

．理由如下：
作OM⊥AC于M，交⊙O于F，如图，
∵AB⊥CD，
∴CH=DH=

1

2

CD=

3

2

，
在Rt△OCH中，OH=

OC2-CH2

=

1

2

，
∴OH=BH，
∴CB=CO=1，
∵OM⊥AC，
∴AM=CM，
∴OM为△ABC的中位线，
∴OM=

1

2

BC=

1

2

，
∴FM=OF-OM=

1

2

，
即在弧AC上点AC的距离为1的点有一个，
而在优弧AEC上到AC的距离为

1

2

的点一定有两个，
∴圆周上存在3个点到直线AC的距离为

1

2

．

点评：本题考查了垂径定理：平分弦的直径平分这条弦，并且平分弦所对的两条弧．也考查了勾股定理．