题目内容
已知在△ABC中，a、b、c分别是∠A、∠B、∠C的对边，如果a=2，b=3，c是方程x2-8x+12=0的根，求△ABC的周长．
考点：解一元二次方程-因式分解法,三角形三边关系
专题：
分析：先求出方程的解，再根据三角形三边关系定理判断，最后求出即可．
解答：解：解x2-8x+12=0得：x1=2，x2=6，
即①三边为a=2，b=3，c=2，符合三角形三边关系定理，即△ABC的周长为2+3+2=7；
②三边为a=2，b=3，c=6，∵2+3＜6，∴不符合三角形三边关系定理，即此时三角形不存在；
综合上述：△ABC的周长为7．
即①三边为a=2，b=3，c=2，符合三角形三边关系定理，即△ABC的周长为2+3+2=7；
②三边为a=2，b=3，c=6，∵2+3＜6，∴不符合三角形三边关系定理，即此时三角形不存在；
综合上述：△ABC的周长为7．
点评：本题考查了解一元二次方程，三角形三边关系定理的应用，解此题的关键是确定c的值，题目比较好，难度适中．
练习册系列答案
相关题目
如图，已知点D、E分别是△ABC边BC、AC上任意一点，AD与BC相交于点F，当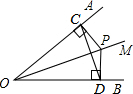
如图，已知OM为∠AOB的平分线，P为OM上一点，PC⊥OA于点C，PD⊥OB于点D，连接CD，请指出图中有几个等腰三角形，并简要说明理由．
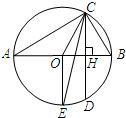如图，AB为⊙O的直径，CD为弦，且CD⊥AB，垂足为H，⊙O的半径为1，CD=
若矩形CDEF相似于矩形ABCD，已知AB=4，BC=8，求矩形CDEF的宽DE．