题目内容
已知在?ABCD中，E是BC上一点，AE交BD于F，S△BEF：S△ADF=4：9，求BE：EC．考点：平行四边形的性质,相似三角形的判定与性质
专题：
分析：求出△BEF和△DAF相似，根据相似三角形面积的比等于相似比的平方求出BE：AD，再根据平行四边形的对边相等可得AD=BC，然后求解即可．
解答：解：在?ABCD中，AD∥BC，
所以，△BEF∽△DAF，
∵S△BEF：S△ADF=4：9，
∴BE：AD=2：3，
∵?ABCD中，AD=BC，
∴BE：BC=2：3，
∴BE：EC=2：1．
所以，△BEF∽△DAF，
∵S△BEF：S△ADF=4：9，
∴BE：AD=2：3，
∵?ABCD中，AD=BC，
∴BE：BC=2：3，
∴BE：EC=2：1．
点评：本题考查了平行四边形的性质，相似三角形的判定与性质，熟记各性质是解题的关键．
练习册系列答案
尖子生新课堂课时作业系列答案
英才计划同步课时高效训练系列答案
相关题目
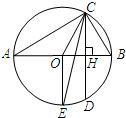如图，AB为⊙O的直径，CD为弦，且CD⊥AB，垂足为H，⊙O的半径为1，CD=
如图，四边形ABCD为直角梯形，∠B=90°，AD=22cm，BC=27cm，点P从A出发，以1cm/s的速度向D运动，点Q从C出发，以2cm/s的速度向B运动，其中一动点达到端点时，另一点随之停止运动．从运动时间开始，经过多少时间四边形PQCD为等腰梯形．