题目内容
10.“若矩形的周长为14,且一边长为3,求另一边的长”;也可以是“若矩形的周长为14,求矩形面积的最大值”,等等.(1)设A=$\frac{3x}{x-2}$-$\frac{x}{x+2}$,B=$\frac{{x}^{2}-4}{x}$,求A与B的积;
(2)提出(1)的一个“逆向”问题,并解答这个问题.
分析 (1)把A与B代入A×B中,约分即可得到结果;
(2)已知A×B,以及B,要求出A,写出解答过程即可.
解答 解:(1)A×B=$\frac{3x(x+2)-x(x-2)}{(x-2)(x+2)}$•$\frac{(x+2)(x-2)}{x}$=2x+8;
(2)已知A×B=2x+8,A=$\frac{3x}{x-2}$-$\frac{x}{x+2}$,求B的值,
根据题意得:B=(2x+8)÷($\frac{3x}{x-2}$-$\frac{x}{x+2}$)=(2x+8)×($\frac{{({x+2})({x-2})}}{{2{x^2}+8x}}$)=$\frac{{x}^{2}-4}{x}$.
点评 此题考查了分式的混合运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
19.九(10)班数学兴趣小组经过市场调查,整理出某种商品在第x(1≤x<50)天的售价与销量的相关信息如下表:
已知该商品的进价为每件10元,设销售该商品的每天利润为y元
(1)求出y与x的函数关系式;
(2)问销售该商品第几天时,当天销售利润最大,最大利润是多少?
(3)该商品在销售过程中,共有多少天每天销售利润不低于2400元?请直接写出结果.
| 时间x(天) | 1≤x<50 | 50≤x≤90 |
| 售价(元/件) | x+40 | 70 |
| 每天销量(件) | 100-2x | |
(1)求出y与x的函数关系式;
(2)问销售该商品第几天时,当天销售利润最大,最大利润是多少?
(3)该商品在销售过程中,共有多少天每天销售利润不低于2400元?请直接写出结果.
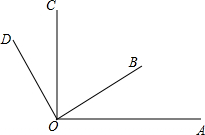 如图,已知∠AOC与∠BOD都是直角,∠BOC=59°.
如图,已知∠AOC与∠BOD都是直角,∠BOC=59°.
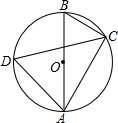 如图,已知AB是⊙O的直径,点C、D在⊙O上,∠D=60°.
如图,已知AB是⊙O的直径,点C、D在⊙O上,∠D=60°.