题目内容
13.已知,如图,AB=AC,AD=AE,∠BAC=∠DAE=90°.(1)求证:△ABD≌△ACE;
(2)求证:BD,CE所在的直线互相垂直;
(3)如图2,连接BE,DC,取BE中点M,连接AM,试判断线段AM与DC有何位置关系,并加以证明.

分析 (1)根据∠BAC=∠DAE,求出∠BAD=∠EAC,根据全等三角形的判定定理SAS即可推出△ABD≌△ACE;
(2)如图1,延长BD,EC交于F,根据全等三角形的性质得到∠ADB=∠AEC,推出A,D,F,E四点共圆,根据圆内接四边形的性质得到∠DAE+∠F=90°,即可得到结论;
(3)延长AM到F,使MF=AM,交CD于点N,构造平行四边形,利用条件证明△ABF≌△CAD,可得出∠BAF=∠ACD,再结合条件可得到∠ANC=90°,可证得结论.
解答 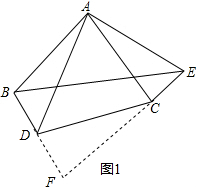 (1)证明:∵∠BAC=∠DAE,
(1)证明:∵∠BAC=∠DAE,
∴∠BAC+∠CAD=∠DAE+∠CAD,
即∠BAD=∠EAC,
在△ABD和△ACE中
$\left\{\begin{array}{l}{AB=AC}\\{∠BAD=∠EAC}\\{AE=AD}\end{array}\right.$,
∴△ABD≌△ACE;
(2)证明:如图1,延长BD,EC交于F,
∵△ABD≌△ACE,
∴∠ADB=∠AEC,
∵∠ADB+∠ADF=180°,
∴∠AEC+∠ADF=180°,
∴A,D,F,E四点共圆,
∴∠DAE+∠F=90°,
∵∠DAE=90°,
∴∠F=90°,
∴BD,CE所在的直线互相垂直;
(3)AM⊥CD,
证明:如图2,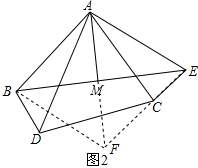 延长AM到F,使MF=AM,交CD于点N,
延长AM到F,使MF=AM,交CD于点N,
∵BM=EM,
∴四边形ABFE是平行四边形,
∴BF=AE,∠ABF+∠BAE=180°,
∵∠BAC=∠DAE=90°,
∴∠CAD+∠BAE=180°,
∴∠ABF=∠CAD,
∵BF=AE,AD=AE,
∴BF=AD,
在△ABF和△CAD中,
$\left\{\begin{array}{l}{BF=AD}\\{∠ABF=CAD}\\{AB=AC}\end{array}\right.$,
∴△ABF≌△CAD(SAS),
∴∠BAF=∠ACD,
∵∠BAC=90°,
∴∠BAF+∠CAM=90°,
∴∠ACD+∠CAN=90°,
∴∠ANC=90°,
∴AM⊥CD.
点评 本题主要考查全等三角形的判定和性质,四点共圆圆内接四边形的性质,通过辅助线构造平行四边形证明三角形全等得到∠BAF=∠ACD是解题的关键.

 阅读快车系列答案
阅读快车系列答案
 如图,直线y=-3x+3与x轴交于点A,与y轴交于点C,点B为x轴正半轴上一点,∠ACB=45°,求点B的坐标(多种方法).
如图,直线y=-3x+3与x轴交于点A,与y轴交于点C,点B为x轴正半轴上一点,∠ACB=45°,求点B的坐标(多种方法). 如图,张华同学在学校某建筑物顶楼的点C处测得正前方小山包上旗杆顶部A点的仰角为26°,旗杆底部B点的俯角为45°,若小山包底部点E到建筑物的水平距离DE=10米.(说明:CD⊥DE于点D,点A、点B、点E在同一直线上,且AE⊥DE于点E)
如图,张华同学在学校某建筑物顶楼的点C处测得正前方小山包上旗杆顶部A点的仰角为26°,旗杆底部B点的俯角为45°,若小山包底部点E到建筑物的水平距离DE=10米.(说明:CD⊥DE于点D,点A、点B、点E在同一直线上,且AE⊥DE于点E)