题目内容
3．
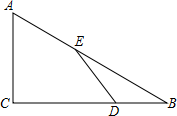如图，Rt△ABC中，∠C=90°，∠B=30°，BA=6，点E在AB边上，点D是BC边上一点（不与点B、C重合），且AE=ED，线段AE的最小值是（ ）| A． | 1 | B． | 2 | C． | 3 | D． | 4 |
分析 以E为圆心，AE的长为半径画圆，当圆与BC相切时，AE最小．根据直角三角形的性质求得结论即可．
解答 
解：以E为圆心，AE的长为半径画圆
如图，当圆E与BC相切时，DE⊥BC时，线段AE的值最小，
∵∠ABC=30°，
∴DE=$\frac{1}{2}$BE，
∵AB=6，
∴AE=2；
故选B．
点评 此题考查了点与圆的位置关系，含30°角的直角三角形的性质，注意根据题意画出图形，结合图形求解是关键．
练习册系列答案
名师点睛字词句段篇系列答案
相关题目
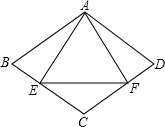如图，菱形ABCD中，E、F分别为BC、CD上的点，△AEF的三边长和菱形边长相等，求∠BAD的大小．
如图，在△ABC中，AB=AC，∠BAC=90°，D为AC边上一点，连接BD，AF⊥BD于点F，点E在BF上，连接AE，∠EAF=45°；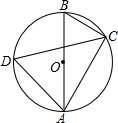
如图，已知AB是⊙O的直径，点C、D在⊙O上，∠D=60°．
12．下列方程中，关于x的一元二次方程是（ ）
| A． | x2+2x=x2-1 | B． | ax2+bx+c=0 | C． | 3（x+1）2=2（x+1） | D． | $\frac{1}{{x}^{2}}$+$\frac{1}{x}$-2=0 |
如图，∠B的同位角是∠ACD，内错角是∠BCE，同旁内角是∠BAC和∠ACB．