题目内容
20.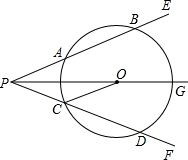 如图所示,射线PG平分∠EPF,O为射线PG上一点,以O为圆心,10为半径作⊙O,分别与∠EPF两边相交于A、B和C、D,连结OA,此时有OC∥PE
如图所示,射线PG平分∠EPF,O为射线PG上一点,以O为圆心,10为半径作⊙O,分别与∠EPF两边相交于A、B和C、D,连结OA,此时有OC∥PE(1)求证:PC=OC;
(2)若弦CD=12,求tan∠OPD的值.
分析 (1)由PG平分∠EPF可得∠CPO=∠APO,由OC∥PE可得∠COP=∠APO,得出∠CPO=∠COP,即可得出结论.
(2)过点O作OH⊥CD于H,如图2.根据垂径定理可得CH=DH=6,从而可求出PH,在Rt△CHO中,运用勾股定理可求出OH,然后运用锐角三角函数的定义就可解决问题.
解答 (1)证明:∵PG平分∠EPF,
∴∠CPO=∠APO.
∵OC∥PE,
∴∠COP=∠APO,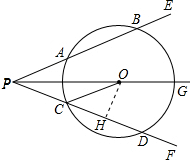
∴∠CPO=∠COP,
∴PC=OC.
(2)解:过点O作OH⊥CD于H,如图所示:
根据垂径定理可得CH=DH=$\frac{1}{2}$CD=6,
∴PH=PC+CH=OC+CH=10+6=16.
在Rt△CHO中,OH=$\sqrt{O{C}^{2}-C{H}^{2}}$=$\sqrt{1{0}^{2}-{6}^{2}}$=8,
∴tan∠OPD=$\frac{OH}{PH}$=$\frac{8}{16}$=$\frac{1}{2}$.
点评 本题考查了垂径定理、等腰三角形的判定与性质、勾股定理、锐角三角函数的定义、平行线的性质、角平分线的定义等知识;熟练掌握垂径定理,由勾股定理求出OH是解决问题(2)的关键.

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
19.九(10)班数学兴趣小组经过市场调查,整理出某种商品在第x(1≤x<50)天的售价与销量的相关信息如下表:
已知该商品的进价为每件10元,设销售该商品的每天利润为y元
(1)求出y与x的函数关系式;
(2)问销售该商品第几天时,当天销售利润最大,最大利润是多少?
(3)该商品在销售过程中,共有多少天每天销售利润不低于2400元?请直接写出结果.
| 时间x(天) | 1≤x<50 | 50≤x≤90 |
| 售价(元/件) | x+40 | 70 |
| 每天销量(件) | 100-2x | |
(1)求出y与x的函数关系式;
(2)问销售该商品第几天时,当天销售利润最大,最大利润是多少?
(3)该商品在销售过程中,共有多少天每天销售利润不低于2400元?请直接写出结果.
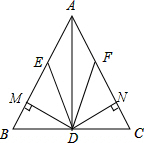 已知,如图,DE∥AC,DF∥AB,AE=AF,DM⊥AB于点M,DN⊥AC于N,求证:DM=DN.
已知,如图,DE∥AC,DF∥AB,AE=AF,DM⊥AB于点M,DN⊥AC于N,求证:DM=DN.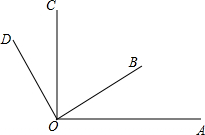 如图,已知∠AOC与∠BOD都是直角,∠BOC=59°.
如图,已知∠AOC与∠BOD都是直角,∠BOC=59°.