题目内容
18. 如图,AD⊥AB,BE⊥AB,AE、BD相交于点C,CF⊥AB,垂足为F.
如图,AD⊥AB,BE⊥AB,AE、BD相交于点C,CF⊥AB,垂足为F.(1)求证:△ADC∽△EBC;
(2)设AD=p,BE=q,CF=r,AF=m,BF=n.用m,n来表示$\frac{r}{p}$,$\frac{r}{q}$;
(3)求证:$\frac{1}{p}$+$\frac{1}{q}$=$\frac{1}{r}$.
分析 (1)由AD⊥AB,BE⊥AB,得到AD∥BE,即可得到结论;
(2)根据AD⊥AB,BE⊥AB,CF⊥AB,于是得到AD∥CF∥BE,证得△FBC∽△ABD,△ACF∽△ABE,得到比例式,即可得到结果;
(3)由(2)知:$\frac{r}{p}=\frac{n}{m+n}$,$\frac{r}{q}=\frac{m}{m+n}$,两式相加即可得到结论.
解答 (1)证明:∵AD⊥AB,BE⊥AB,
∴AD∥BE,
∴△ADC∽△EBC;
(2)解:∵AD⊥AB,BE⊥AB,CF⊥AB,
∴AD∥CF∥BE,
∴△FBC∽△ABD,△ACF∽△ABE,
∴$\frac{CF}{AD}=\frac{BF}{AB}$,$\frac{CF}{BE}=\frac{AF}{AB}$,
即:$\frac{r}{p}=\frac{n}{m+n}$,$\frac{r}{q}=\frac{m}{m+n}$;
(3)证明:由(2)知:$\frac{r}{p}=\frac{n}{m+n}$,$\frac{r}{q}=\frac{m}{m+n}$,
∴$\frac{r}{p}+\frac{r}{q}$=$\frac{n}{m+n}$+$\frac{m}{m+n}$=$\frac{m+n}{m+n}$=1,
∴$\frac{1}{p}$+$\frac{1}{q}$=$\frac{1}{r}$.
点评 本题考查了相似三角形的判定和性质,熟练掌握相似三角形的判定和性质是解题的关键.

练习册系列答案
相关题目
8.在下列条件中,能判定四边形ABCD为平行四边形的是( )
| A. | AB=AD,CB=CD | B. | AB∥CD,AD=BC | C. | AB=CD,AD=BC | D. | ∠A=∠B,∠C=∠D |
6. 已知二次函数y=ax2+bx+c的图象如图所示,则a的取值范围为( )
已知二次函数y=ax2+bx+c的图象如图所示,则a的取值范围为( )
 已知二次函数y=ax2+bx+c的图象如图所示,则a的取值范围为( )
已知二次函数y=ax2+bx+c的图象如图所示,则a的取值范围为( )| A. | -1<a<0 | B. | -1<a<$\frac{5}{2}$ | C. | 0<a<$\frac{5}{2}$ | D. | $\frac{1}{2}$<a<$\frac{5}{8}$ |
 四边形ABCD是正方形,E在正方形外,CE∥BD,EB=BD,BE交DC于F,
四边形ABCD是正方形,E在正方形外,CE∥BD,EB=BD,BE交DC于F,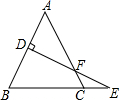 如图,△ABC中,AB=AC,AB的垂直平分线DE交BC的延长线于E,交AC于F,∠A=50°,AB+BC=6cm,则△BCF的周长为6cm,∠EFC的度数为40°.
如图,△ABC中,AB=AC,AB的垂直平分线DE交BC的延长线于E,交AC于F,∠A=50°,AB+BC=6cm,则△BCF的周长为6cm,∠EFC的度数为40°.