题目内容
13. 四边形ABCD是正方形,E在正方形外,CE∥BD,EB=BD,BE交DC于F,
四边形ABCD是正方形,E在正方形外,CE∥BD,EB=BD,BE交DC于F,求证:
(1)∠BEC=30°;
(2)DE=DF.
分析 (1)过点B作BG⊥CE交EC的延长线于G,证出△BCG是等腰直角三角形,根据等腰直角三角形的性质求出BG=$\frac{1}{2}$BD=$\frac{1}{2}$BE,由三角函数即可得出结论;
(2)由平行线的性质得出∠DBE=∠BEC=30°,求出∠CBF=15°,得出∠DFE=75°,由等腰三角形的性质得出∠BED=∠BDE=75°,得出∠BED=∠DFE,即可得出DE=DF.
解答 证明:(1)过点B作BG⊥CE交EC的延长线于G,如图所示: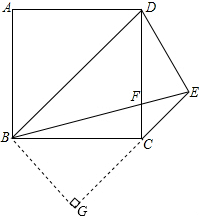
∵四边形ABCD是正方形,
∴∠CBD=45°,BC=$\frac{\sqrt{2}}{2}$BD,
∵CE∥BD,
∴∠BCG=∠CBD=45°,
∴△BCG是等腰直角三角形,
∴BG=$\frac{\sqrt{2}}{2}$BC=$\frac{\sqrt{2}}{2}$×$\frac{\sqrt{2}}{2}$BD=$\frac{1}{2}$BD,
∵EB=BD,
∴BG=$\frac{1}{2}$BE,
又∵BG⊥CE,
∴sin∠BEC=$\frac{1}{2}$,
∴∠BEC=30°.
(2)∵CE∥BD,
∴∠DBE=∠BEC=30°,
∴∠CBF=45°-30°=15°,
∴∠DFE=∠BFC=90°-15°=75°,
∵EB=BD,
∴∠BED=∠BDE=75°,
∴∠BED=∠DFE,
∴DE=DF.
点评 本题考查了正方形的性质、等腰直角三角形的判定与性质、三角函数;熟练掌握正方形的性质,并能进行推理论证与计算是解决问题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
3.有一道四选一的数学题,小强同学全靠猜,那么他猜中的概率是( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{6}$ |
3.若抛物线y=(x+1)2+c与y轴相交于点(0,-5),则y的最小值为( )
| A. | -6 | B. | 6 | C. | -5 | D. | 5 |
 已知一次函数y=-2x+7的图象与x轴、y轴分别交于点A、B.
已知一次函数y=-2x+7的图象与x轴、y轴分别交于点A、B.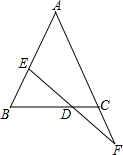 已知:如图,D是EF的中点,BE=CF,求证:△ABC是等腰三角形.
已知:如图,D是EF的中点,BE=CF,求证:△ABC是等腰三角形. 如图,AD⊥AB,BE⊥AB,AE、BD相交于点C,CF⊥AB,垂足为F.
如图,AD⊥AB,BE⊥AB,AE、BD相交于点C,CF⊥AB,垂足为F.