题目内容
6.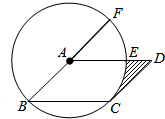 如图,在?ABCD中,以点A为圆心,AB的长为半径的圆恰好与CD相切于点C,交AD于点E,延长BA与⊙O相交于点F.若$\widehat{EF}$的长为$\frac{π}{2}$,则图中阴影部分的面积为2-$\frac{π}{2}$.
如图,在?ABCD中,以点A为圆心,AB的长为半径的圆恰好与CD相切于点C,交AD于点E,延长BA与⊙O相交于点F.若$\widehat{EF}$的长为$\frac{π}{2}$,则图中阴影部分的面积为2-$\frac{π}{2}$.
分析 连结AC,如图,设半径为r,先根据切线的性质得∠ACD=90°,再根据平行四边形的性质得AB∥CD,AD∥BC,则∠CAF=90°,∠1=∠B,∠2=∠3,利用∠B=∠3易得∠1=∠2=45°,则根据弧长公式可得$\frac{45•π•r}{180}$=$\frac{π}{2}$,解得r=2,然后根据扇形面积公式,利用S阴影部分=S△ACD-S扇形CAE进行计算即可.
解答 解: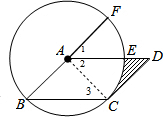 连结AC,如图,设半径为r,
连结AC,如图,设半径为r,
∵AB的长为半径的圆恰好与CD相切于点C,
∴AC⊥CD,
∴∠ACD=90°,
∵四边形ABCD为平行四边形,
∴AB∥CD,AD∥BC,
∴∠CAF=90°,∠1=∠B,∠2=∠3,
而AB=AC,
∴∠B=∠3,
∴∠1=∠2=45°,
∵$\widehat{EF}$的长为$\frac{π}{2}$,
∴$\frac{45•π•r}{180}$=$\frac{π}{2}$,解得r=2,
在Rt△ACD中,∵∠2=45°,
∴AC=CD=2,
∴S阴影部分=S△ACD-S扇形CAE$\frac{1}{2}$×2×2-$\frac{45•π•{2}^{2}}{360}$=2-$\frac{π}{2}$.
故答案为2-$\frac{π}{2}$.
点评 本题考查了切线的性质:圆的切线垂直于经过切点的半径.也考查了平行四边形的性质和扇形的面积公式.

练习册系列答案
相关题目
14.抛物线y=x2-2x+1向左平移2个单位长度后,所得到的抛物线与x轴的交点坐标为( )
| A. | (-3,0) | B. | (-2,0) | C. | (-1,0) | D. | (3,0) |
11.有下列四种说法:
(1)过直线外一点有且只有一条直线与这条直线平行
(2)平面内,过一点能且只能作一条直线与已知直线垂直
(3)直线外一点与直线上各点连接的所有线段中,垂线段最短
(4)平行于同一条直线的两条直线平行.
其中正确的个数是( )
(1)过直线外一点有且只有一条直线与这条直线平行
(2)平面内,过一点能且只能作一条直线与已知直线垂直
(3)直线外一点与直线上各点连接的所有线段中,垂线段最短
(4)平行于同一条直线的两条直线平行.
其中正确的个数是( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
16.某工厂生产一种合金薄板(其厚度忽略不计),这些薄板的形状均为正方形,边长在(单位:cm)在5~50之间.每张薄板的成本价(单位:元)与它的面积(单位:cm2)成正比例,每张薄板的出厂价(单位:元)有基础价和浮动价两部分组成,其中基础价与薄板的大小无关,是固定不变的.浮动价与薄板的边长成正比例.在营销过程中得到了表格中的数据.已知出厂一张边长为40cm的薄板,获得的利润为26元.
(1)求一张薄板的出厂价与边长之间满足的函数关系式;
(2)若一张薄板的利润是34元,且成本最低,此时薄板的边长为多少?
(3)若限定薄板的边长不超过20cm,浮动价下降a%,其他条件不变,薄板的利润随边长的增加而增大时,直接写出a的取值范围.
| 薄板的边长(cm) | 20 | 30 |
| 出厂价(元/张) | 50 | 70 |
(2)若一张薄板的利润是34元,且成本最低,此时薄板的边长为多少?
(3)若限定薄板的边长不超过20cm,浮动价下降a%,其他条件不变,薄板的利润随边长的增加而增大时,直接写出a的取值范围.
 如图,将平面直角坐标系的纵轴绕原点顺时针旋转30°,得到夹角为60°的平面坐标系xOy,称之为平面60°角坐标系.类比平面直角坐标系中确定点的坐标的方法,设平面60°角坐标系中有任意一点P,过点P作PA∥y轴,交x轴于点A,A点的坐标为(x,0),过点P作PB∥x轴,交y轴于点B,B点的坐标为(0,y),则点P坐标为(x,y).
如图,将平面直角坐标系的纵轴绕原点顺时针旋转30°,得到夹角为60°的平面坐标系xOy,称之为平面60°角坐标系.类比平面直角坐标系中确定点的坐标的方法,设平面60°角坐标系中有任意一点P,过点P作PA∥y轴,交x轴于点A,A点的坐标为(x,0),过点P作PB∥x轴,交y轴于点B,B点的坐标为(0,y),则点P坐标为(x,y).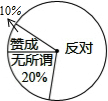 “校园手机”现象越来越受到社会的关注,“五一”期间,小记者刘涵随机调查了城区若干名家长对中学生带手机现象的看法,统计整理并制作了如图的统计图,家长“反对”的圆心角的度数是252°.
“校园手机”现象越来越受到社会的关注,“五一”期间,小记者刘涵随机调查了城区若干名家长对中学生带手机现象的看法,统计整理并制作了如图的统计图,家长“反对”的圆心角的度数是252°. 如图,直线AB,CD被BC所截,E是BC上一点,连接DE.若AB∥CD,∠1=45°,∠2=35°,则∠3=80度.
如图,直线AB,CD被BC所截,E是BC上一点,连接DE.若AB∥CD,∠1=45°,∠2=35°,则∠3=80度.