题目内容
6. 如图,在平面直角坐标系xOy中,反比例函数y=$\frac{m}{x}$的图象与一次函数y=k(x-2)的图象交点为A(3,2),B(x,y).
如图,在平面直角坐标系xOy中,反比例函数y=$\frac{m}{x}$的图象与一次函数y=k(x-2)的图象交点为A(3,2),B(x,y).(1)求反比例函数与一次函数的解析式及B点坐标;
(2)若C是y轴上的点,且满足△ABC的面积为10,求C点坐标.
分析 (1)根据点A(3,2)在反比例函数y=$\frac{m}{x}$,和一次函数y=k(x-2)上列出m和k的一元一次方程,求出k和m的值即可;联立两函数解析式,求出交点坐标;
(2)设C点的坐标为(0,yc),求出点M的坐标,再根据△ABC的面积为10,知$\frac{1}{2}$×3×|yc-(-4)|+$\frac{1}{2}$×1×|yc-(-4)|=10,求出yc的值即可.
解答 解:(1)∵点A(3,2)在反比例函数y=$\frac{m}{x}$,和一次函数y=k(x-2)上;
∴2=$\frac{m}{3}$,2=k(3-2),解得m=6,k=2;
∴反比例函数解析式为y=$\frac{6}{x}$,和一次函数解析式为y=2x-4;
∵点B是一次函数与反比例函数的另一个交点,
∴$\frac{6}{x}$=2x-4,解得x1=3,x2=-1;
∴B点的坐标为(-1,6);
(2)∵点M是一次函数y=2x-4与y轴的交点,
∴点M的坐标为(0,-4),
设C点的坐标为(0,yc),由题意知$\frac{1}{2}$×3×|yc-(-4)|+$\frac{1}{2}$×1×|yc-(-4)|=10,
解得|yc+4|=5,
当yc+4≥0时,yc+4=5,解得yc=1,
当yc+4≤0时,yc+4=-5,解得yc=-9,
∴点C的坐标为(0,1)或(0,-9).
点评 本题主要考查了反比例函数与一次函数的交点问题,解题的关键是求出两个函数的解析式以及直线AB与y轴的交点坐标,此题难度一般.

练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目
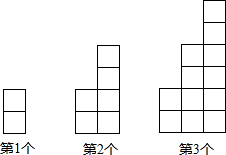 如图,每个图案都由大小相同的正方形组成,按照此规律,第n个图案中这样的正方形的总个数可用含n的代数式表示为n(n+1).
如图,每个图案都由大小相同的正方形组成,按照此规律,第n个图案中这样的正方形的总个数可用含n的代数式表示为n(n+1). 如图,两同心圆的大圆半径长为5cm,小圆半径长为3cm,大圆的弦AB与小圆相切,切点为C,则弦AB的长是8cm.
如图,两同心圆的大圆半径长为5cm,小圆半径长为3cm,大圆的弦AB与小圆相切,切点为C,则弦AB的长是8cm.