题目内容
20.设a,b为实数,且a<b,则下列不等式变形正确的是( )| A. | 3a<3b | B. | -a<-b | C. | a+1>b+1 | D. | $\frac{a}{2}>\frac{b}{2}$ |
分析 首先根据不等式的两边同时乘以(或除以)同一个正数,不等号的方向不变,可得3a<3b正确,$\frac{a}{2}>\frac{b}{2}$错误;然后根据不等式的两边同时乘以(或除以)同一个负数,不等号的方向改变,可得-a>-b,选项B错误;最后根据不等式的两边同时加上(或减去)同一个数或同一个含有字母的式子,不等号的方向不变,可得a+1>b+1错误,据此解答即可.
解答 解:∵a<b,
∴3a<3b,$\frac{a}{2}<\frac{b}{2}$,
即选项A正确,选项D错误;
∵a<b,
∴-a>-b,
即选项B错误;
∵a<b,
∴a+1<b+1,
即选项C错误;
故选:A.
点评 此题主要考查了不等式的基本性质:(1)不等式的两边同时乘以(或除以)同一个正数,不等号的方向不变;(2)不等式的两边同时乘以(或除以)同一个负数,不等号的方向改变;(3)不等式的两边同时加上(或减去)同一个数或同一个含有字母的式子,不等号的方向不变.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
11.⊙O的内接正三角形的边长等于3$\sqrt{3}$,则⊙O的面积等于( )
| A. | 27π | B. | $\frac{27}{4}$π | C. | 9π | D. | $\frac{9}{4}$π |
8.化简(-a2)5+(-a5)2的结果( )
| A. | -2a7 | B. | 0 | C. | a | D. | -2a10 |
9.下列说法正确的是( )
| A. | 64的立方根是±$\root{3}{64}$=±$\sqrt{4}$ | B. | -$\frac{1}{2}$是-$\frac{1}{6}$的立方根 | ||
| C. | $\root{3}{-27}$=-$\root{3}{27}$ | D. | 立方根等于它本身的数是0和1 |
10.计算a2•a5,正确的结果是( )
| A. | 2a7 | B. | 2a10 | C. | a7 | D. | a10 |
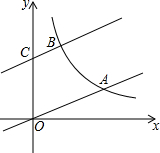 如图,直线y=$\frac{1}{3}$x与双曲线y=$\frac{k}{x}$(k>0,x>0)交于点A,将直线y=$\frac{1}{3}$x向上平移3个单位得到直线y=ax+b,它与y轴交于点C,与双曲线y=$\frac{k}{x}$(k>0,x>0)交于点B.若OA=2BC.
如图,直线y=$\frac{1}{3}$x与双曲线y=$\frac{k}{x}$(k>0,x>0)交于点A,将直线y=$\frac{1}{3}$x向上平移3个单位得到直线y=ax+b,它与y轴交于点C,与双曲线y=$\frac{k}{x}$(k>0,x>0)交于点B.若OA=2BC.