题目内容
19. 已知:如图,点G是CA的延长线上一点,CE交AB于点F,AD∥GE,且∠AGF=∠AFG.求证:AD平分∠BAC.
已知:如图,点G是CA的延长线上一点,CE交AB于点F,AD∥GE,且∠AGF=∠AFG.求证:AD平分∠BAC.
分析 先根据三角形外角性质,得到∠BAD+∠CAD=∠AGF+∠AFG,再根据平行线的性质,得出∠BAD=∠AFG,∠CAD=∠G,根据∠AGF=∠AFG,可得∠BAD=∠CAD,即可得出AD平分∠BAC.
解答 证明:∵∠BAC=∠BAD+∠CAD,∠BAC=∠AGF+∠AFG,
∴∠BAD+∠CAD=∠AGF+∠AFG,
又∵AD∥GE,
∴∠BAD=∠AFG,∠CAD=∠G,
∵∠AGF=∠AFG,
∴∠BAD=∠CAD,
∴AD平分∠BAC.
点评 本题主要考查了平行线的性质以及角平分线的定义的运用,解题时注意:两直线平行,同位角相等,内错角相等.

练习册系列答案
相关题目
 如图,等腰△ABC中,AB=AC,∠DBC=15°,AB的垂直平分线MN交AC于点D,则∠A的度数?
如图,等腰△ABC中,AB=AC,∠DBC=15°,AB的垂直平分线MN交AC于点D,则∠A的度数?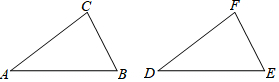
 已知:△ABC内部一点O到两边AB、AC所在直线的距离相等,且OB=OC.
已知:△ABC内部一点O到两边AB、AC所在直线的距离相等,且OB=OC. 如图,矩形ABCD中,AB=4,BC=6,E是BC上一点(不与B、C重合),点P在边CD上运动,M、N分别是AE、PE的中点,线段MN长度的最大值是$\sqrt{13}$.
如图,矩形ABCD中,AB=4,BC=6,E是BC上一点(不与B、C重合),点P在边CD上运动,M、N分别是AE、PE的中点,线段MN长度的最大值是$\sqrt{13}$.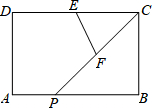 如图,矩形△ABCD中,AB=2,AD=1,E为CD中点,P为AB边上一动点(含端点),F为CP中点,则△CEF的周长最小值为$\sqrt{2}$+1.
如图,矩形△ABCD中,AB=2,AD=1,E为CD中点,P为AB边上一动点(含端点),F为CP中点,则△CEF的周长最小值为$\sqrt{2}$+1.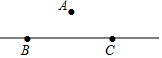 如图,高速公路BC(公路视为直线)的最高限速为120km/h,在该公路正上方离地面20m的点A处设置了一个测速仪,已知在点A测得点B的俯角为45°,点C的俯角为30°,测速仪监测到一辆汽车从点B匀速行驶到点C所用的时间是1.5s,试通过计算,判决该汽车在这段限速路上是否超速.(参考数据:$\sqrt{3}$≈1.7)
如图,高速公路BC(公路视为直线)的最高限速为120km/h,在该公路正上方离地面20m的点A处设置了一个测速仪,已知在点A测得点B的俯角为45°,点C的俯角为30°,测速仪监测到一辆汽车从点B匀速行驶到点C所用的时间是1.5s,试通过计算,判决该汽车在这段限速路上是否超速.(参考数据:$\sqrt{3}$≈1.7)