Question

13．非直角三角形ABC中，∠A=50°，高BE，CF所在的直线交于点O，求∠BOC的度数．

Answer 1

分析 本题中因为“高BE、CF所在直线交于点O，且点E、F不与点B、C重合”排除了三角形是直角三角形的可能，所以要分两种情况讨论．

解答 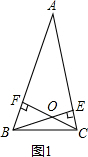解：本题要分两种情况讨论如图：
①当交点在三角形内部时（如1），
在四边形AFOE中，∠AFC=∠AEB=90°，∠A=50°，
根据四边形内角和等于360°得，
∠EOF=180°-∠A=180°-50°=130°．
故∠BOC=130°．
②当交点在三角形外部时（如图2），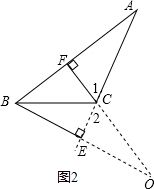
在△AFC中，∠A=50°，∠AFC=90°，
故∠1=180°-90°-50°=40°，
∵∠1=∠2，
∴在△CEO中，∠2=40°，∠CEO=90°，
∴∠EOF=180°-90°-40°=70°，即∠BOC=50°．

点评 本题考查的是三角形内角和定理，在解答此题时要注意进行分类讨论，不要漏解．