题目内容
18．若n！=n（n-1）×（n-2）×（n-3）×…×3×2×1，则$\frac{n!}{（n+2）!}$=$\frac{1}{（n+2）（n+1）}$．分析 根据定义列出算式，然后再约分即可．
解答 解：$\frac{n!}{（n+2）!}=\frac{n（n-1）×（n-2）（n-3）×…×3×2×1}{（n+2）（n+1）×n（n-1）×…×3×2×1}$=$\frac{1}{（n+2）（n+1）}$．
故答案为：$\frac{1}{（n+2）（n+1）}$
点评 本题主要考查的是有理数的乘法和除法，根据定义列出算式，然后将分母和分子中的相同因式约去是解题的关键．
练习册系列答案
相关题目
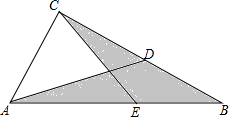在△ABC中，AE=2EB，D为BC的中点，△ACD的面积为$\frac{1}{4}$，△BCE的面积为$\frac{1}{6}$，求阴影部分的面积．
甲乙两地相距300千米，一辆货车和一辆轿车先后从甲地出发向乙地如图、线段OA表示货车离甲地距离y（千米）与时间x（小时）之间的函数关系；折线BCD表示货车离甲地距离y（千米）与时间x（小时）之间的函数关系，根据图象解答下列问题：
10．计算3a3•（-2a）2的结果是（ ）
| A． | 12a5 | B． | -12a5 | C． | 12a6 | D． | -12a6 |