题目内容
18.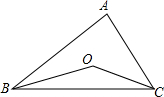 如图,在△ABC中,∠ABC、∠ACB的平分线交于O点.
如图,在△ABC中,∠ABC、∠ACB的平分线交于O点.①当∠A=20°时,∠BOC=100°;
②当∠A=40°时,∠BOC=110°;
③当∠A=60°时,∠BOC=120°;
④∠A=n°时,猜测∠BOC=90°+$\frac{1}{2}$•n°,
并用所学的三角形的有关知识把④进行说明.
分析 运用三角形内角和定理,由∠A可求出∠ABC+∠ACB,根据角平分线定义就可求出∠OBC+∠OCB,再运用三角形内角和定理就可求出∠BOC.
解答 解:①当∠A=20°时,∠ABC+∠ACB=180°-∠A=160°.
∵BO平分∠ABC,CO平分∠ACB,
∴∠OBC=$\frac{1}{2}$∠ABC,∠OCB=$\frac{1}{2}$∠ACB,
∴∠OBC+∠OCB=$\frac{1}{2}$∠ABC+$\frac{1}{2}$∠ACB=$\frac{1}{2}$(∠ABC+∠ACB)=80°,
∴∠BOC=180°-(∠OBC+∠OCB)=100°.
②当∠A=40°时,同理可得∠BOC=110°;
③当∠A=60°时,同理可得∠BOC=120°;
④当∠A=n°时,同理可得∠BOC=90°+$\frac{1}{2}$•n°.
故答案分别为:①100°;②110°;③120°;④90°+$\frac{1}{2}$•n°.
④的理由:当∠A=n°时,∠ABC+∠ACB=180°-n°.
∵BO平分∠ABC,CO平分∠ACB,
∴∠OBC=$\frac{1}{2}$∠ABC,∠OCB=$\frac{1}{2}$∠ACB,
∴∠OBC+∠OCB=$\frac{1}{2}$∠ABC+$\frac{1}{2}$∠ACB=$\frac{1}{2}$(∠ABC+∠ACB)=$\frac{1}{2}$(180°-n°)=90°-$\frac{1}{2}$•n°,
∴∠BOC=180°-(∠OBC+∠OCB)=180°-(90°-$\frac{1}{2}$•n°)=90°+$\frac{1}{2}$•n°.
点评 本题主要考查了角平分线的定义,三角形内角和定理等知识,运用三角形内角和定理,把∠BOC转化为∠A是解决本题的关键.

 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案| A. | 1$\frac{1}{2}$ | B. | $\frac{2}{3}$ | C. | -1$\frac{1}{2}$ | D. | -$\frac{2}{3}$ |
| A. | 正数 | B. | 负数 | C. | 非负数 | D. | 非正数 |
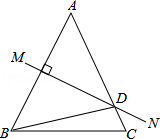 如图,等腰△ABC中,AB=AC,∠DBC=15°,AB的垂直平分线MN交AC于点D,则∠C的度数是65°.
如图,等腰△ABC中,AB=AC,∠DBC=15°,AB的垂直平分线MN交AC于点D,则∠C的度数是65°.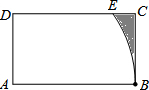 如图,在矩形ABCD中,AB=4,AD=2,以点A为圆心,AB长为半径画圆弧交边DC于点E,则阴影部分的面积是8-2$\sqrt{3}$-$\frac{4π}{3}$(结果保留π).
如图,在矩形ABCD中,AB=4,AD=2,以点A为圆心,AB长为半径画圆弧交边DC于点E,则阴影部分的面积是8-2$\sqrt{3}$-$\frac{4π}{3}$(结果保留π). 如图,已知△ABC≌△DBE,如果∠CBD=96°,∠CBE=28°,那么∠ABC=68°.
如图,已知△ABC≌△DBE,如果∠CBD=96°,∠CBE=28°,那么∠ABC=68°.