题目内容
8.已知a2-6a+9与(b-1)2互为相反数,则式子($\frac{a}{b}-\frac{b}{a}$)÷(a+b)的值是$\frac{2}{3}$.分析 由互为相反数的意义,可得:(a-3)2+(b-1)2=0,然后由非负数的性质可得a、b的值,然后解答即可.
解答 解:∵a2-6a+9与(b-1)2互为相反数,
∴(a-3)2+(b-1)2=0,
∵(a-3)2≥0,(b-1)2≥0,
∴a=3,b=1,
∴($\frac{a}{b}-\frac{b}{a}$)÷(a+b)=(3-$\frac{1}{3}$)÷(3+1)=$\frac{2}{3}$.
故答案为:$\frac{2}{3}$.
点评 考查了配方法的应用,非负数的性质及代数式求值的知识,解题的关键是能够对代数式进行正确的配方,难道不大.

练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
19.有理数|-3|的相反数是( )
| A. | $\frac{1}{3}$ | B. | -$\frac{1}{3}$ | C. | 3 | D. | -3 |
17.下列性质中正方形具有而矩形没有的是( )
| A. | 对角线互相平分 | B. | 对角线相等 | ||
| C. | 对角线平分一组对角 | D. | 四个角都是直角 |
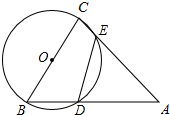 如图:△ABC中,∠A=60°,以BC为直径作半圆,交AB于D,交AC于E.求证:DE=$\frac{1}{2}$BC.
如图:△ABC中,∠A=60°,以BC为直径作半圆,交AB于D,交AC于E.求证:DE=$\frac{1}{2}$BC.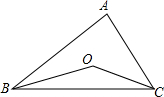 如图,在△ABC中,∠ABC、∠ACB的平分线交于O点.
如图,在△ABC中,∠ABC、∠ACB的平分线交于O点.