题目内容
6.$-1\frac{1}{2}$的倒数是( )| A. | 1$\frac{1}{2}$ | B. | $\frac{2}{3}$ | C. | -1$\frac{1}{2}$ | D. | -$\frac{2}{3}$ |
分析 求一个数的倒数,即1除以这个数.
解答 解:$-1\frac{1}{2}$的倒数是$-\frac{2}{3}$.
故选D.
点评 此题考查了倒数的性质,要求掌握倒数的定义,并能熟练运用到实际当中.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
17.下列性质中正方形具有而矩形没有的是( )
| A. | 对角线互相平分 | B. | 对角线相等 | ||
| C. | 对角线平分一组对角 | D. | 四个角都是直角 |
1.用一种正多边形铺满地面时,不能铺满地面的是( )
| A. | 正三边形 | B. | 正八边形 | C. | 正六边形 | D. | 正四边形 |
15.初步探索 感悟方法
如图1,用水平线和竖直线将平面分成若干个边长为1的小正方形格子,小正方形的顶点,叫格点,以格点为顶点的多边形叫格点多边形,设格点多边形的面积为S,它各边上格点的个数和为x.
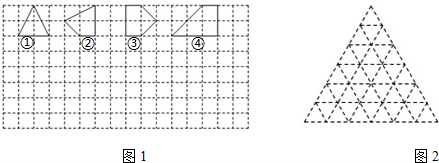
(1)如图1中所示的格点多边形,其内部都只有一个格点,它们的面积与各边上格点的个数和的对应关系如下表,请填写下表并写出S与x之间的关系式,答:S=$\frac{1}{2}$x.
(2)你可以画些格点多边形,使这些多边形内部都有而且只有2个格点.
此时所画的各个多边形的面积S与它各边上格点的个数和x之间的关系式S=$\frac{1}{2}$x+1.
(3)请你继续探索,当格点多边形内部有且只有n(n是正整数)个格点时,猜想S与x、n之间的关系式S=$\frac{1}{2}$x+(n-1)..(用含有字母x、n的代数式表示)
积累经验 拓展延伸
如图2,对等边三角形网格中的类似问题进行探究:等边三角形网格中每个小等边三角形的面积为1,小等边三角形的顶点为格点,以格点为顶点的多边形称为格点多边形.
(4)设格点多边形的面积为S,它各边上格点的个数和为x,当格点多边形内部有且只有n个格点时,猜想S与x、n之间的关系式S=x+2(n-1).(用含有字母x、n的代数式表示)
如图1,用水平线和竖直线将平面分成若干个边长为1的小正方形格子,小正方形的顶点,叫格点,以格点为顶点的多边形叫格点多边形,设格点多边形的面积为S,它各边上格点的个数和为x.

(1)如图1中所示的格点多边形,其内部都只有一个格点,它们的面积与各边上格点的个数和的对应关系如下表,请填写下表并写出S与x之间的关系式,答:S=$\frac{1}{2}$x.
| 多边形的序号 | ① | ② | ③ | ④ | … |
| 多边形的面积S | 2 | 2.5 | 3 | 4 | … |
| 各边上格点的个数和x | 4 | 5 | 6 | 8 | … |
此时所画的各个多边形的面积S与它各边上格点的个数和x之间的关系式S=$\frac{1}{2}$x+1.
(3)请你继续探索,当格点多边形内部有且只有n(n是正整数)个格点时,猜想S与x、n之间的关系式S=$\frac{1}{2}$x+(n-1)..(用含有字母x、n的代数式表示)
积累经验 拓展延伸
如图2,对等边三角形网格中的类似问题进行探究:等边三角形网格中每个小等边三角形的面积为1,小等边三角形的顶点为格点,以格点为顶点的多边形称为格点多边形.
(4)设格点多边形的面积为S,它各边上格点的个数和为x,当格点多边形内部有且只有n个格点时,猜想S与x、n之间的关系式S=x+2(n-1).(用含有字母x、n的代数式表示)
 已知矩形ABCD中,在BC上取一点E,沿AE将△ABE向上折叠,使B点落在AD上的F点,且四边形EFDC与矩形ABCD相似.
已知矩形ABCD中,在BC上取一点E,沿AE将△ABE向上折叠,使B点落在AD上的F点,且四边形EFDC与矩形ABCD相似.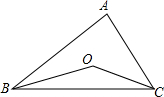 如图,在△ABC中,∠ABC、∠ACB的平分线交于O点.
如图,在△ABC中,∠ABC、∠ACB的平分线交于O点.