题目内容
10.选择适当方法解下列方程:(1)x2-4x+1=0(用配方法);
(2)3x(x-1)=2-2x
(3)(x-2)(x-3)=12
(4)2x2-2$\sqrt{2}$x-5=0(公式法).
分析 (1)利用配方法得到(x-2)2=3,然后利用直接开平方法解方程;
(2)先变形得到3x(x-1)+2(x-1)=0,然后利用因式分解法解方程;
(3)先把方程化为一般式,然后利用因式分解法解方程;
(4)利用求根公式法解方程.
解答 解:(1)x2-4x=-1,
x2-4x+4=-1+4,
(x-2)2=3,
x-2=$±\sqrt{3}$
所以x1=$2+\sqrt{3}$,x2=$2-\sqrt{3}$;
(2)3x(x-1)=2(1-x),
3x(x-1)+2(x-1)=0
(x-1)(3x+2)=0,
x-1=0或3x+2=0,
所以x1=1; x2=-$\frac{3}{2}$;
(3)x2-5x+6=12,
x2-5x-6=0,
(x-6)(x+1)=0,
所以x1=6; x2=-1,
(4)解方程:2x2-2$\sqrt{2}$x-5=0;
x=$\frac{2\sqrt{2}±\sqrt{8-4×2×(-5)}}{4}$ …(2分)
所以x1=$\frac{\sqrt{2}+2\sqrt{3}}{2}$; x2=$\frac{\sqrt{2}-2\sqrt{3}}{2}$.
点评 本题考查了解一元二次方程-因式分解法:先把方程的右边化为0,再把左边通过因式分解化为两个一次因式的积的形式,那么这两个因式的值就都有可能为0,这就能得到两个一元一次方程的解,这样也就把原方程进行了降次,把解一元二次方程转化为解一元一次方程的问题了(数学转化思想).也考查了配方法和公式法解一元二次方程.

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
1.用一种正多边形铺满地面时,不能铺满地面的是( )
| A. | 正三边形 | B. | 正八边形 | C. | 正六边形 | D. | 正四边形 |
15.初步探索 感悟方法
如图1,用水平线和竖直线将平面分成若干个边长为1的小正方形格子,小正方形的顶点,叫格点,以格点为顶点的多边形叫格点多边形,设格点多边形的面积为S,它各边上格点的个数和为x.
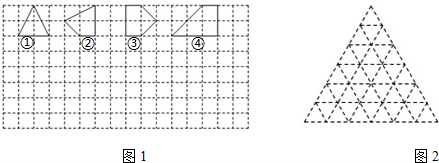
(1)如图1中所示的格点多边形,其内部都只有一个格点,它们的面积与各边上格点的个数和的对应关系如下表,请填写下表并写出S与x之间的关系式,答:S=$\frac{1}{2}$x.
(2)你可以画些格点多边形,使这些多边形内部都有而且只有2个格点.
此时所画的各个多边形的面积S与它各边上格点的个数和x之间的关系式S=$\frac{1}{2}$x+1.
(3)请你继续探索,当格点多边形内部有且只有n(n是正整数)个格点时,猜想S与x、n之间的关系式S=$\frac{1}{2}$x+(n-1)..(用含有字母x、n的代数式表示)
积累经验 拓展延伸
如图2,对等边三角形网格中的类似问题进行探究:等边三角形网格中每个小等边三角形的面积为1,小等边三角形的顶点为格点,以格点为顶点的多边形称为格点多边形.
(4)设格点多边形的面积为S,它各边上格点的个数和为x,当格点多边形内部有且只有n个格点时,猜想S与x、n之间的关系式S=x+2(n-1).(用含有字母x、n的代数式表示)
如图1,用水平线和竖直线将平面分成若干个边长为1的小正方形格子,小正方形的顶点,叫格点,以格点为顶点的多边形叫格点多边形,设格点多边形的面积为S,它各边上格点的个数和为x.

(1)如图1中所示的格点多边形,其内部都只有一个格点,它们的面积与各边上格点的个数和的对应关系如下表,请填写下表并写出S与x之间的关系式,答:S=$\frac{1}{2}$x.
| 多边形的序号 | ① | ② | ③ | ④ | … |
| 多边形的面积S | 2 | 2.5 | 3 | 4 | … |
| 各边上格点的个数和x | 4 | 5 | 6 | 8 | … |
此时所画的各个多边形的面积S与它各边上格点的个数和x之间的关系式S=$\frac{1}{2}$x+1.
(3)请你继续探索,当格点多边形内部有且只有n(n是正整数)个格点时,猜想S与x、n之间的关系式S=$\frac{1}{2}$x+(n-1)..(用含有字母x、n的代数式表示)
积累经验 拓展延伸
如图2,对等边三角形网格中的类似问题进行探究:等边三角形网格中每个小等边三角形的面积为1,小等边三角形的顶点为格点,以格点为顶点的多边形称为格点多边形.
(4)设格点多边形的面积为S,它各边上格点的个数和为x,当格点多边形内部有且只有n个格点时,猜想S与x、n之间的关系式S=x+2(n-1).(用含有字母x、n的代数式表示)
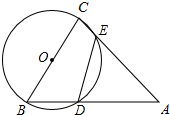 如图:△ABC中,∠A=60°,以BC为直径作半圆,交AB于D,交AC于E.求证:DE=$\frac{1}{2}$BC.
如图:△ABC中,∠A=60°,以BC为直径作半圆,交AB于D,交AC于E.求证:DE=$\frac{1}{2}$BC.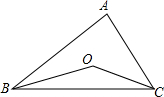 如图,在△ABC中,∠ABC、∠ACB的平分线交于O点.
如图,在△ABC中,∠ABC、∠ACB的平分线交于O点. 已知:如图,在△ABC中,AB=AC,点D在AB上,且CB=CD=AD,求:△CBD各角的度数.
已知:如图,在△ABC中,AB=AC,点D在AB上,且CB=CD=AD,求:△CBD各角的度数.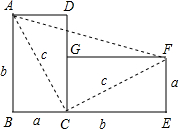 如图,将边长为a与b、对角线长为c的长方形纸片ABCD,绕点C顺时针旋转90°得到长方形FGCE,连接AF.通过用不同方法计算梯形ABEF的面积可验证一条我们学过的定理,该定理的名称是勾股定理,请你写出验证的过程.
如图,将边长为a与b、对角线长为c的长方形纸片ABCD,绕点C顺时针旋转90°得到长方形FGCE,连接AF.通过用不同方法计算梯形ABEF的面积可验证一条我们学过的定理,该定理的名称是勾股定理,请你写出验证的过程.