题目内容
在△ABC中，∠C=90°，AC=3，AB=5，若以A、B、C、P四点为顶点组成一个平行四边形，则这个平行四边形的周长为 ．
考点：平行四边形的判定
专题：
分析：先利用勾股定理求出BC的长，然后分类讨论即可确定答案．
解答：解：∵△ABC中，∠C=90°，AC=3，AB=5，
∴BC=4，
当以AB为对角线时，此时?ACBP的周长为（3+4）×2=14；
当以AC为对角线时，此时?APCB的周长为（5+4）×2=18；
当以BC为对角线时，此时?ACPB的周长为（5+3）×2=16；
故答案为：14或16或18．
∴BC=4，
当以AB为对角线时，此时?ACBP的周长为（3+4）×2=14；
当以AC为对角线时，此时?APCB的周长为（5+4）×2=18；
当以BC为对角线时，此时?ACPB的周长为（5+3）×2=16；
故答案为：14或16或18．
点评：本题考查了平行四边形的判定，解题的关键是分类讨论．
练习册系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
如图，△ABC中，AB=5，BC=11，tanB=
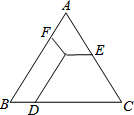如图，△ABC是等边三角形，P是形内一点，PD∥AB，PE∥BC，PF∥AC，若△ABC的周长为18，则PD+PE+PF=（ ）| A、18 | ||
B、9
| ||
| C、6 | ||
| D、条件不够，不能确定 |
如图，在直角梯形ABCD中，DC∥AB，∠DAB=90°，AC⊥BC，AC=BC，∠ABC的平分线分别交AD、AC于点E，F，则| BF |
| EF |
A、
| ||
B、2+
| ||
C、
| ||
D、
|