题目内容
10.已知二次函数y=x2+bx+c(其中b,c为常数,c>0)的顶点恰为函数y=2x和y=$\frac{2}{x}$的其中一个交点.则当a2+ab+c>2a>$\frac{2}{a}$时,a的取值范围是-1<a<0或a>3.分析 只需先求出抛物线的顶点坐标,再求出抛物线与直线y=2x的交点,然后结合函数图象就可解决问题.
解答 解:解方程组$\left\{\begin{array}{l}{y=2x}\\{y=\frac{2}{x}}\end{array}\right.$,得
$\left\{\begin{array}{l}{{x}_{1}=1}\\{{y}_{1}=2}\end{array}\right.$,$\left\{\begin{array}{l}{{x}_{2}=-1}\\{{y}_{2}=-2}\end{array}\right.$.
①当抛物线y=x2+bx+c顶点为(1,2)时,
抛物线的解析式为y=(x-1)2+2=x2-2x+3.
解方程组$\left\{\begin{array}{l}{y={x}^{2}-2x+3}\\{y=2x}\end{array}\right.$,得
$\left\{\begin{array}{l}{{x}_{1}=1}\\{{y}_{1}=2}\end{array}\right.$,$\left\{\begin{array}{l}{{x}_{2}=3}\\{{y}_{2}=6}\end{array}\right.$.
结合图象可得: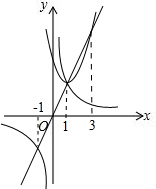
当a2+ab+c>2a>$\frac{2}{a}$时,a的取值范围是-1<a<0或a>3;
②当抛物线y=x2+bx+c顶点为(-1,-2)时,
抛物线的解析式为y=(x+1)2-2=x2+2x-1.
∴c=-1<0,与条件c>0矛盾,故舍去.
故答案为-1<a<0或a>3.
点评 本题主要考查了直线与反比例函数图象的交点、抛物线的顶点坐标公式、直线与抛物线的交点等知识,运用数形结合的思想是解决本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
1.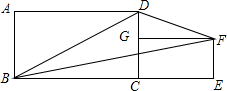 矩形ABCD中,AB=4,BC=8,矩形CEFG上的点G在CD边,EF=a,CE=2a,连接BD、BF、DF,则△BDF的面积是( )
矩形ABCD中,AB=4,BC=8,矩形CEFG上的点G在CD边,EF=a,CE=2a,连接BD、BF、DF,则△BDF的面积是( )
 矩形ABCD中,AB=4,BC=8,矩形CEFG上的点G在CD边,EF=a,CE=2a,连接BD、BF、DF,则△BDF的面积是( )
矩形ABCD中,AB=4,BC=8,矩形CEFG上的点G在CD边,EF=a,CE=2a,连接BD、BF、DF,则△BDF的面积是( )| A. | 32 | B. | 16 | C. | 8 | D. | 16+a2 |
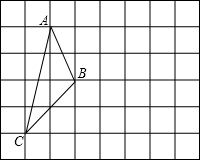 如图,在方格纸中,每个小正方形的边长均为1个单位长度有一个△ABC,它的三个顶点均与小正方形的顶点重合.
如图,在方格纸中,每个小正方形的边长均为1个单位长度有一个△ABC,它的三个顶点均与小正方形的顶点重合.