题目内容
4．
如图，在△ABC中，∠C=90°，分别以点A，B为圆心，大于$\frac{1}{2}$AB长为半径作弧，两弧分别交于M，N两点，过M，N两点的直线交AC于点E，若AC=8，BC=6，则AE的长为（ ）| A． | 2 | B． | 3 | C． | $\frac{24}{5}$ | D． | $\frac{25}{4}$ |
分析 根据题意可知直线MN是线段AB的垂直平分线，故可得出AE=BE，设AE=BE=x，则CE=AC-x=8-x，在Rt△BCE中利用勾股定理求出x的值即可．
解答 解：∵由题意可知直线MN是线段AB的垂直平分线，
∴AE=BE．
设AE=BE=x，则CE=AC-x=8-x，
在Rt△BCE中，
∵BC2+CE2=BE2，即62+（8-x）2=x2，解得x=$\frac{25}{4}$．
故选D．
点评 本题考查的是作图-基本作图，熟知线段垂直平分线的作法是解答此题的关键．
练习册系列答案
阅读快车系列答案
相关题目
15．2017年春节黄金周宜春市共接待游客2234000人次，将2234000用科学记数法表示为（ ）
| A． | 22.34×105 | B． | 2.234×105 | C． | 2.234×106 | D． | 0.2234×107 |
12．对于问题：证明不等式a2+b2≥2ab，甲、乙两名同学的作业如下：
甲：根据一个数的平方是非负数可知（a-b）2≥0，
∴a2-2ab+b2≥0，
∴a2+b2≥2ab．
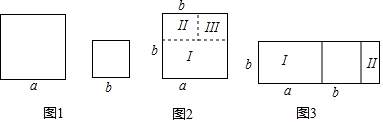
乙：如图1，两个正方形的边长分别为a、b（b≤a），如图2，先将边长为a的正方形沿虚线部分分别剪成Ⅰ、Ⅱ、Ⅲ三部分，若再将Ⅰ、Ⅱ和边长为b的正方形拼接成如图3所示的图形，可知此时图3的面积为2ab，其面积小于或等于原来两个正方形的面积和，故不等式a2+b2≥2ab成立．
则对于两人的作业，下列说法正确的是（ ）
甲：根据一个数的平方是非负数可知（a-b）2≥0，
∴a2-2ab+b2≥0，
∴a2+b2≥2ab．
乙：如图1，两个正方形的边长分别为a、b（b≤a），如图2，先将边长为a的正方形沿虚线部分分别剪成Ⅰ、Ⅱ、Ⅲ三部分，若再将Ⅰ、Ⅱ和边长为b的正方形拼接成如图3所示的图形，可知此时图3的面积为2ab，其面积小于或等于原来两个正方形的面积和，故不等式a2+b2≥2ab成立．
则对于两人的作业，下列说法正确的是（ ）
| A． | 甲、乙都对 | B． | 甲对，乙不对 | C． | 甲不对，乙对 | D． | 甲、乙都不对 |
19．中国的数学研究具有悠久的历史，《九章算术》是我国的一部古典数学名著，但对其成书的年代说法不一，一般认为在公元前后，距今约2 000年．将2 000用科学记数法表示为（ ）
| A． | 2×103 | B． | 2×104 | C． | 20×103 | D． | 0.2×103 |
16．如果关于x的不等式（2a+1）x＜2a+1的解集为x＞1，那么a的取值范围是（ ）
| A． | a＞0 | B． | a＜0 | C． | a＞-$\frac{1}{2}$ | D． | a＜-$\frac{1}{2}$ |
我市某小区实施供暖改造工程，现甲、乙两工程队分别同时开挖两条600米长的管道，所挖管道长度y（米）与挖掘时间x（天）之间的关系如图所示，则下列说法中，正确的个数有（ ）个．