题目内容
16．如果关于x的不等式（2a+1）x＜2a+1的解集为x＞1，那么a的取值范围是（ ）| A． | a＞0 | B． | a＜0 | C． | a＞-$\frac{1}{2}$ | D． | a＜-$\frac{1}{2}$ |
分析 由不等号的方向即可求出a的值．
解答 解：由题意可知：2a+1＜0
∴a＜-$\frac{1}{2}$
故选（D）
点评 本题考查不等式的性质，解题的关键是正确理解不等式的性质，本题属于基础题型．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
6．定义新运算：对于任意实数a、b都有a?b=|3a-b|，则x?1-x?2的值为（ ）
| A． | -2 | B． | -1 | C． | -$\frac{3}{2}$ | D． | 0 |
7．某玩具厂生产一种玩具，本着控制固定成本，降价促销的原则，使生产的玩具能够全部售出．据市场调查，若按每个玩具280元销售时，每月可销售300个．若销售单价每降低1元，每月可多售出2个．据统计，每个玩具的固定成本Q（元）与月产销量y（个）满足如下关系：
（1）每月产销量y（个）与销售单价x（元）之间的函数关系式为y=-2x+860；从上表可知，每个玩具的固定成本Q（元）与月产销量y（个）之间满足反比例函数关系式，求出Q与y之间的关系式；
（2）若每个玩具的固定成本为30元，求它的销售单价是多少元？
（3）若该厂这种玩具的月产销量不超过400个，求此时销售单价最低为多少元？
| 月产销量y（个） | … | 160 | 200 | 240 | 300 | … |
| 每个玩具的固定成本Q（元） | … | 60 | 48 | 40 | 32 | … |
（2）若每个玩具的固定成本为30元，求它的销售单价是多少元？
（3）若该厂这种玩具的月产销量不超过400个，求此时销售单价最低为多少元？
4．
如图，在△ABC中，∠C=90°，分别以点A，B为圆心，大于$\frac{1}{2}$AB长为半径作弧，两弧分别交于M，N两点，过M，N两点的直线交AC于点E，若AC=8，BC=6，则AE的长为（ ）
如图，在△ABC中，∠C=90°，分别以点A，B为圆心，大于$\frac{1}{2}$AB长为半径作弧，两弧分别交于M，N两点，过M，N两点的直线交AC于点E，若AC=8，BC=6，则AE的长为（ ）| A． | 2 | B． | 3 | C． | $\frac{24}{5}$ | D． | $\frac{25}{4}$ |
在四边形OABC中，AB∥OC，BC⊥x轴于C，A（1，-1），B（3，-1），动点P从O点出发，沿x轴正方向以2个单位/秒的速度运动．过P作PQ⊥OA于Q．设P点运动的时间为t秒（0＜t＜2），△OPQ与四边形OABC重叠的面积为S．
1．-$\frac{1}{9}$的倒数是（ ）
| A． | 9 | B． | -9 | C． | $\frac{1}{9}$ | D． | -1 |
已知：如图，在正方形ABCD中，点E、F分别在BC和CD上，BE=DF．
5．
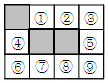在由相同的小正方形组成的3×4的网格中，有3个小正方形已经涂黑，请你再涂黑一个小正方形，使涂黑的四个小正方形构成的图形为轴对称图形，则还需要涂黑的小正方形序号是（ ）
在由相同的小正方形组成的3×4的网格中，有3个小正方形已经涂黑，请你再涂黑一个小正方形，使涂黑的四个小正方形构成的图形为轴对称图形，则还需要涂黑的小正方形序号是（ ）| A． | ①或② | B． | ③或⑥ | C． | ④或⑤ | D． | ③或⑨ |
6．下列图形中既是轴对称图形又是中心对称图形的是（ ）
| A． |  | B． |  | C． |  | D． |  |