题目内容
7.等腰直角三角形T的面积为正方形S的两倍,则T的一条直角边与S边长之比为?分析 设等腰直角三角形的直角边为a,正方形S的边长为b(a、b均为正数),根据等腰直角三角形T的面积为正方形S的两倍即可得出$\frac{1}{2}$a2=2b2,解之即可得出a:b=±2,取其正值即可得出结论.
解答 解:设等腰直角三角形的直角边为a,正方形S的边长为b(a、b均为正数),
根据题意得:$\frac{1}{2}$a2=2b2,
∴a:b=2或a:b=-2(舍去).
答:T的一条直角边与S边长之比为2.
点评 本题考查了正方形的性质以及等腰直角三角形,根据两图形面积间的关系找出a与b之间的关系是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
16.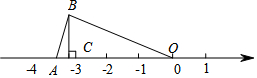 如图,OA=OB,BC=1,则数轴上点A所表示的数为( )
如图,OA=OB,BC=1,则数轴上点A所表示的数为( )
 如图,OA=OB,BC=1,则数轴上点A所表示的数为( )
如图,OA=OB,BC=1,则数轴上点A所表示的数为( )| A. | $\sqrt{10}$ | B. | $\sqrt{5}$ | C. | $-\sqrt{10}$ | D. | -3.5 |
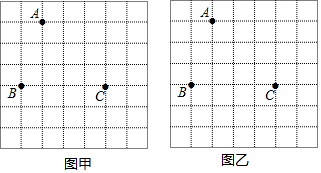
 已知:如图,AB=CD,AD=BC.求证:AB∥CD.
已知:如图,AB=CD,AD=BC.求证:AB∥CD. 如图,直线EF过边长为5的正方形ABCD的顶点B,点A、C到直线EF的距离分别是3和4,则五边形AEFCD的面积是37.
如图,直线EF过边长为5的正方形ABCD的顶点B,点A、C到直线EF的距离分别是3和4,则五边形AEFCD的面积是37. 如图,已知AD=BC,AC=BD.请探究:OA与OB是否相等?若相等,请证明;若不相等,请说明理由.
如图,已知AD=BC,AC=BD.请探究:OA与OB是否相等?若相等,请证明;若不相等,请说明理由.