题目内容
15.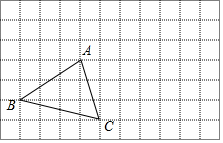 在正方形网格中,每个小正方形的边长均为1个单位长度,△ABC的三个顶点的位置如图所示,△ABC先向右平移5格,再向上平移3格,得到△A1B1C1.
在正方形网格中,每个小正方形的边长均为1个单位长度,△ABC的三个顶点的位置如图所示,△ABC先向右平移5格,再向上平移3格,得到△A1B1C1.(1)在图中画出△A1B1C1;
(2)网格线的交点(即小正方形的顶点)称为格点,在图中找出格点P和格点Q,连接AP、AQ,使AP⊥BC,AQ∥B1C1;
(3)在图中探究并求得△ABC的面积=5.5(直接写出结果).
分析 (1)直接利用平移的性质得出对应点位置进而得出答案;
(2)直接利用网格结合垂直的性质以及平行线的性质得出答案;
(3)直接利用△ABC所在矩形面积减去周围三角形面积进而得出答案.
解答  解:(1)如图所示:△A1B1C1,即为所求;
解:(1)如图所示:△A1B1C1,即为所求;
(2)如图所示:AP,AQ即为所求;
(3)△ABC的面积=3×4-$\frac{1}{2}$×2×3-$\frac{1}{2}$×1×4-$\frac{1}{2}$×1×3=5.5.
故答案为:5.5.
点评 此题主要考查了平移的变换以及三角形面积求法,正确得出对应点位置是解题关键.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目
10.下面各条件中,能判定四边形是平行四边形的是( )
| A. | 对角线互相垂直 | B. | 两组对边分别相等 | ||
| C. | 一组对角相等 | D. | 一组对边相等,另一组对边平行 |
20.下列图形既是中心对称图形又是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
7.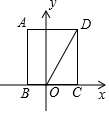 如图,矩形ABCD的边BC在x轴上,点A在第二象限,点D在第一象限,AB=2$\sqrt{3}$,OD=4,将矩形ABCD绕点O旋转,使点D落在x轴上,则点C对应点的坐标是( )
如图,矩形ABCD的边BC在x轴上,点A在第二象限,点D在第一象限,AB=2$\sqrt{3}$,OD=4,将矩形ABCD绕点O旋转,使点D落在x轴上,则点C对应点的坐标是( )
 如图,矩形ABCD的边BC在x轴上,点A在第二象限,点D在第一象限,AB=2$\sqrt{3}$,OD=4,将矩形ABCD绕点O旋转,使点D落在x轴上,则点C对应点的坐标是( )
如图,矩形ABCD的边BC在x轴上,点A在第二象限,点D在第一象限,AB=2$\sqrt{3}$,OD=4,将矩形ABCD绕点O旋转,使点D落在x轴上,则点C对应点的坐标是( )| A. | (-$\sqrt{3}$,1) | B. | (-1,$\sqrt{3}$) | C. | (-1,$\sqrt{3}$)或(1,-$\sqrt{3}$) | D. | (-$\sqrt{3}$,1)或(1,-$\sqrt{3}$) |
 端午节是我国四大传统文化节日之一,为每年的农历五月初五,自古以来端午节便有划龙舟及食粽等习俗.重庆某大型超市为了了解市民对“蛋黄粽”的喜好程度,特意在三峡广场做了试吃及问卷调查活动,将市民对“蛋黄粽”的喜好程度分为“A非常喜欢”、“B比较喜欢”、“C感觉一般”、“D不太喜欢”四个等级,并将四个等级分别计分为:A等级10分,B等级7分,C等级5分,D等级2分,根据调查结果绘制出如图所示的条形统计图,请问“蛋黄粽”的平均分是7分.
端午节是我国四大传统文化节日之一,为每年的农历五月初五,自古以来端午节便有划龙舟及食粽等习俗.重庆某大型超市为了了解市民对“蛋黄粽”的喜好程度,特意在三峡广场做了试吃及问卷调查活动,将市民对“蛋黄粽”的喜好程度分为“A非常喜欢”、“B比较喜欢”、“C感觉一般”、“D不太喜欢”四个等级,并将四个等级分别计分为:A等级10分,B等级7分,C等级5分,D等级2分,根据调查结果绘制出如图所示的条形统计图,请问“蛋黄粽”的平均分是7分.