题目内容
 如图,经过原点的直线交双曲线y=-
如图,经过原点的直线交双曲线y=-| 3 |
| x |
| k |
| x |
| CD |
| OP |
| 2 |
| 3 |
考点:反比例函数与一次函数的交点问题
专题:
分析:设P(a,-
),则D(-
,-
),C(a,
).连接AB,进而得出
=
=
,再证明△CPD∽△APB,根据相似三角形对应边成比例得到
=
=
,那么可用含a的代数式表示C点坐标,进而得出答案.
| 3 |
| a |
| ak |
| 3 |
| 3 |
| a |
| k |
| a |
| PC |
| PA |
| 3+k |
| 3 |
| PD |
| PB |
| PC |
| PA |
| CD |
| AB |
| 2 |
| 3 |
解答: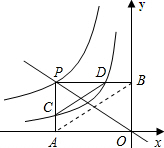 解:设P(a,-
解:设P(a,-
),则D(-
,-
),C(a,
).
连接AB,在矩形OAPB中,∵OP=AB,
∴
=
=
,
∵
=
=
,且∠CPD=∠APB,
∴△CPD∽△APB,
∴
=
=
,
∴PC=
PA=
×(-
)=-
,
∴AC=PA-PC=-
-(-
)=-
,
∴C(a,-
).
∵双曲线y=
(x<0)经过点C,
∴k=a×(-
)=-1.
故答案为-1.
 解:设P(a,-
解:设P(a,-| 3 |
| a |
| ak |
| 3 |
| 3 |
| a |
| k |
| a |
连接AB,在矩形OAPB中,∵OP=AB,
∴
| CD |
| AB |
| CD |
| OP |
| 2 |
| 3 |
∵
| PC |
| PA |
| 3+k |
| 3 |
| PD |
| PB |
∴△CPD∽△APB,
∴
| PC |
| PA |
| CD |
| AB |
| 2 |
| 3 |
∴PC=
| 2 |
| 3 |
| 2 |
| 3 |
| 3 |
| a |
| 2 |
| a |
∴AC=PA-PC=-
| 3 |
| a |
| 2 |
| a |
| 1 |
| a |
∴C(a,-
| 1 |
| a |
∵双曲线y=
| k |
| x |
∴k=a×(-
| 1 |
| a |
故答案为-1.
点评:此题主要考查了反比例函数与一次函数的交点问题以及相似三角形的性质和判定,计算得出
=
=
,进而表示出C点坐标是解题关键.
| PC |
| PA |
| 3+k |
| 3 |
| PD |
| PB |

练习册系列答案
相关题目
 如图,在△ABC中,D为BC边的中点,点E在线段AD上,BE的延长线交AC边于点F,若AE:ED=1:3,AF=2,求线段FC的长.
如图,在△ABC中,D为BC边的中点,点E在线段AD上,BE的延长线交AC边于点F,若AE:ED=1:3,AF=2,求线段FC的长. 已知如图,四边形ABCD的边长是2的菱形,且∠CDA=30°,CF⊥x轴,求点D关于CF的对称点D′的坐标.
已知如图,四边形ABCD的边长是2的菱形,且∠CDA=30°,CF⊥x轴,求点D关于CF的对称点D′的坐标. 如图,在△ABC中,以AC为直径的⊙O交BC于D,过C作⊙O的切线,交AB的延长线于P,∠PCB=
如图,在△ABC中,以AC为直径的⊙O交BC于D,过C作⊙O的切线,交AB的延长线于P,∠PCB= 如图,已知AB=AC,∠A=36°,AB的中垂线MN交AC于点D,交AB于点M,
如图,已知AB=AC,∠A=36°,AB的中垂线MN交AC于点D,交AB于点M, 如图,已知△ABC中AB=AC,BD、CD分别平分∠EBA、∠ECA,BD交AC于F,连接AD,
如图,已知△ABC中AB=AC,BD、CD分别平分∠EBA、∠ECA,BD交AC于F,连接AD, 如图,矩形ABCO,点E在AB上,且BE=2AE,点F在BC上,双曲线y=
如图,矩形ABCO,点E在AB上,且BE=2AE,点F在BC上,双曲线y= 实数a,b在数轴上所对应的点的位置如图所示,化简|b-a|-
实数a,b在数轴上所对应的点的位置如图所示,化简|b-a|-