题目内容
 已知如图,四边形ABCD的边长是2的菱形,且∠CDA=30°,CF⊥x轴,求点D关于CF的对称点D′的坐标.
已知如图,四边形ABCD的边长是2的菱形,且∠CDA=30°,CF⊥x轴,求点D关于CF的对称点D′的坐标.考点:菱形的性质,坐标与图形性质
专题:
分析:先解直角三角形求出CF和DF的长,根据轴对称性质求出求出AF,再求出D′A的长,即可得出答案.
解答:解: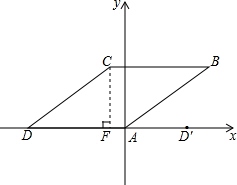
∵四边形ABCD的边长是2的菱形,
∴DC=AD=2,
∵CF⊥x轴,
∴∠CFD=90°,
∵∠CDA=30°,
∴CF=
DC=1,
由勾股定理得:DF=
=
,
∵点D关于CF的对称点D′,
∴DF=D′F=
,
∴AF=AD-DF=2-
,
∴D′A=DF′-AF=
-(2-
)=2
-2,
即点D关于CF的对称点D′的坐标为(2
-2,0).

∵四边形ABCD的边长是2的菱形,
∴DC=AD=2,
∵CF⊥x轴,
∴∠CFD=90°,
∵∠CDA=30°,
∴CF=
| 1 |
| 2 |
由勾股定理得:DF=
| 22-12 |
| 3 |
∵点D关于CF的对称点D′,
∴DF=D′F=
| 3 |
∴AF=AD-DF=2-
| 3 |
∴D′A=DF′-AF=
| 3 |
| 3 |
| 3 |
即点D关于CF的对称点D′的坐标为(2
| 3 |
点评:本题考查了菱形的性质,勾股定理,含30度角的直角三角形的性质,轴对称性质的应用,能综合运用性质进行推理和计算是解此题的关键,难度适中.

练习册系列答案
相关题目
 如图,已知矩形OABC的面积为25,它的对角线OB与双曲线
如图,已知矩形OABC的面积为25,它的对角线OB与双曲线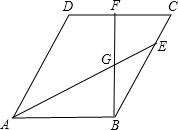 如图,平行四边形ABCD中,AE平分∠DAB,BF⊥DC交AE于点G,且BF=AB
如图,平行四边形ABCD中,AE平分∠DAB,BF⊥DC交AE于点G,且BF=AB 如图,将两个长方形叠在一起,得到四个正方形和一个长方形ABCD,已知四个正方形的面积和为60,长方形ABCD的周长为12,求长方形ABCD的面积.
如图,将两个长方形叠在一起,得到四个正方形和一个长方形ABCD,已知四个正方形的面积和为60,长方形ABCD的周长为12,求长方形ABCD的面积. 如图,线段AD、BC相交于点E,AB⊥BC,BC⊥DC,BE=120,EC=60,DC=50,求AB的长.
如图,线段AD、BC相交于点E,AB⊥BC,BC⊥DC,BE=120,EC=60,DC=50,求AB的长. 如图△ABC内接于⊙O,AD平分∠BAC,交⊙O于点K,过点A作⊙O的切线交CB的延长线于点E
如图△ABC内接于⊙O,AD平分∠BAC,交⊙O于点K,过点A作⊙O的切线交CB的延长线于点E 如图,经过原点的直线交双曲线
如图,经过原点的直线交双曲线 如图,在宽为20m,长为32m的长方形地面上修同样宽的两条不规则的路,余下的部分为耕地,若小路宽均为2m,求耕地面积为多少?
如图,在宽为20m,长为32m的长方形地面上修同样宽的两条不规则的路,余下的部分为耕地,若小路宽均为2m,求耕地面积为多少? 如图,三角形ABC中,E,G是AC上的点,D,F是BC上的点,AB∥ED,ED⊥AC,GF⊥AC,求证:AB∥GF.
如图,三角形ABC中,E,G是AC上的点,D,F是BC上的点,AB∥ED,ED⊥AC,GF⊥AC,求证:AB∥GF.