Question

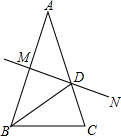如图，已知AB=AC，∠A=36°，AB的中垂线MN交AC于点D，交AB于点M，
（1）写出图中所有的相似三角形；
（2）从（1）中选出一对相似比不为1的相似三角形加以证明．

Answer 1

考点：相似三角形的判定,线段垂直平分线的性质,等腰三角形的性质

专题：计算题

分析：（1）根据题意得到相似三角形，写出即可；
（2）选择相似比不为1的三角形ABC与三角形BCD相似，利用两对角相等的三角形相似证明即可．

解答：解：（1）根据题意得：△ABC∽△BCD，△AMD∽△BMD；
（2）△ABC∽△BCD，理由如下：
∵AB=AC，∠A=36°，
∴∠ABC=∠C=72°，
∵MN垂直平分AB，
∴AD=BD，
∴∠ABD=∠A=36°，
∵∠A=∠CBD=36°，∠C=∠C，
∴△ABC∽△BCD．

点评：此题考查了相似三角形的判定，线段垂直平分线的性质，以及等腰三角形的性质，熟练掌握相似三角形的判定方法是解本题的关键．