题目内容
2.已知关于x的方程2x2-(4k+1)x+2k2-1=0,则当k取何值时:(1)方程有两个不等的实数根?
(2)方程有两个相等的实数根?并求此时方程的实数根.
(3)方程没有实数根?
分析 根据根的判别式即可求出k的取值.
解答 解:由题意可知:△=(4k+1)2-4×2×(2k2-1)=8k+9,
(1)∵方程有两个不等的实数根,
∴△>0,
∴8k+9>0,
∴k>-$\frac{9}{8}$
(2)∵方程有两个相等的实数根,
∴△=0,
∴k=-$\frac{9}{8}$,
由求根公式可知:x=-$\frac{b}{2a}$=$\frac{4k-1}{4}$=-$\frac{11}{8}$
(3)∵方程没有实数根
∴△<0,
∴k<-$\frac{9}{8}$
点评 本题考查根的判别式,解题的关键是正确理解判别式的作用,本题属于基础题型.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
10.NBA季后赛正如火如荼地进行着,詹姆斯率领的骑士队在第三场季后赛中先落后25分的情况下实现了大逆转.该场比赛中詹姆斯的技术统计数据如下表所示:
(表中投篮次数和投中次数均不包括罚球,个人总得分来自2分球和3分球的得分以及罚球得分)根据以上信息,求出本场比赛中詹姆斯投中2分球和3分球的个数.
| 技术 | 上场时间 | 投篮次数 | 投中次数 | 罚球得分 | 篮板个数 | 助攻次数 | 个人总得分 |
| 数据 | 45 | 27 | 14 | 7 | 13 | 12 | 41 |
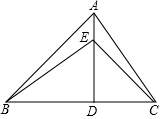 如图,锐角△ABC中,∠ABC=45°,AD是高,E为AD上一点,BE=AC.
如图,锐角△ABC中,∠ABC=45°,AD是高,E为AD上一点,BE=AC. 如图所示,在平面直角坐标系中,OA1=1,将OA1以O为旋转中心逆时针旋转90°到y轴OA2处,然后半径增加1个单位长度到A3,将OA3再以点O为旋转中心逆时针旋转90°到x轴OA4处,然后半径增加1个单位长度到A5,…,按图中规律进行下去,则点A2017的坐标为(1010,0).
如图所示,在平面直角坐标系中,OA1=1,将OA1以O为旋转中心逆时针旋转90°到y轴OA2处,然后半径增加1个单位长度到A3,将OA3再以点O为旋转中心逆时针旋转90°到x轴OA4处,然后半径增加1个单位长度到A5,…,按图中规律进行下去,则点A2017的坐标为(1010,0).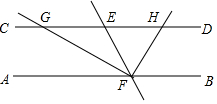 如图,直线EF分别与直线AB,CD相交于点F,E,FG平分∠AFE交CD于点G,FH平分∠BFE交CD于点H,若∠GEF=7∠FGE,AB∥CD,那么∠HFB=70°.
如图,直线EF分别与直线AB,CD相交于点F,E,FG平分∠AFE交CD于点G,FH平分∠BFE交CD于点H,若∠GEF=7∠FGE,AB∥CD,那么∠HFB=70°.