题目内容
15.在数学课上,老师给出这样一个问题:如图1,在平行四边形ABCD中,AB<BC.利用尺规作图,在边BC上确定一点E为圆心作圆,使⊙E与边AB,AD都相切(不写作法,保留作图痕迹);

小刚是这样思考的:(如图2)
(1)作∠BAD的平分线与BC边交于点E;
(2)过点E作边AD的垂线,垂足为点F;
(3)以点E为圆心,EF长为半径作圆即可;
小刚把想法和老师交流了,得到了老师的肯定和赞扬,请你回答:小刚这样做的依据是角平分线上的点到角的两边的距离相等.
分析 先由作法得出AD与⊙E相切,再根据角平分线上的点到角的两边的距离相等判断出AB也与⊙E相切,
解答 解:如图,
过E作EG⊥AB于G,
∵AE平分∠BAD,FE⊥AD,
∴EG=EF,
∵EF是⊙E的半径,
∴AB与⊙E相切;
故答案为:角平分线上的点到角的两边的距离相等.
点评 此题是切线的性质,主要考查了基本作图,角平分线的性质定理,切线的判定,解本题的关键是审清题意,用点到的直线的距离等于半径来判定直线是圆的切线.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4.使分式$\frac{{{x^2}-4}}{x-2}$无意义的x的取值是( )
| A. | x=±2 | B. | x=2 | C. | x=-2 | D. | x=0 |
 已知:如图,在△ABC中,AB=BC,D是AC中点,BE平分∠ABD交AC于点E,点O是AB上一点,⊙O过B、E两点,交BD于点G,交AB于点F. BD=6,sinC=$\frac{3}{5}$.则下面结论正确的有(填序号)(1)(2)
已知:如图,在△ABC中,AB=BC,D是AC中点,BE平分∠ABD交AC于点E,点O是AB上一点,⊙O过B、E两点,交BD于点G,交AB于点F. BD=6,sinC=$\frac{3}{5}$.则下面结论正确的有(填序号)(1)(2)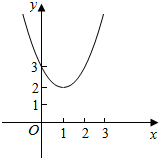 如图,二次函数y=ax2+bx+c(a≠0)的图象经过点(0,3),且当x=1时,y有最小值2.
如图,二次函数y=ax2+bx+c(a≠0)的图象经过点(0,3),且当x=1时,y有最小值2.
