��Ŀ����
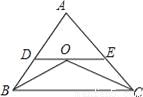
��֪����ͼ����ABC�У�BO��CO�ֱ��ǡ�ABC�͡�ACB��ƽ���ߣ���O���ֱ�߷ֱ�AB��AC�ڵ�D��E����DE��BC����AB=6cm��AC=8cm�����ADE���ܳ�Ϊ__��

 14cm
����������ֱ��ƽ�У��ڴ�����ȣ��Լ����ݽ�ƽ�������ʣ��ɵá�OBD����EOC��Ϊ���������Σ��ɴ˰ѡ�AEF���ܳ�ת��ΪAC+AB��
��������
��DE��BC�����DOB=��OBC���֡�BO�ǡ�ABC�Ľ�ƽ���ߣ����DBO=��OBC�����DBO=��DOB����BD=OD��ͬ����OE=EC��
���ADE���ܳ�=AD+OD+OE+EC=AD+BD+AE+EC=AB+AC=14c...
14cm
����������ֱ��ƽ�У��ڴ�����ȣ��Լ����ݽ�ƽ�������ʣ��ɵá�OBD����EOC��Ϊ���������Σ��ɴ˰ѡ�AEF���ܳ�ת��ΪAC+AB��
��������
��DE��BC�����DOB=��OBC���֡�BO�ǡ�ABC�Ľ�ƽ���ߣ����DBO=��OBC�����DBO=��DOB����BD=OD��ͬ����OE=EC��
���ADE���ܳ�=AD+OD+OE+EC=AD+BD+AE+EC=AB+AC=14c...
��ͼ���߶�AB�ij�Ϊ2��CΪAB��һ�����㣬�ֱ���AC��BCΪб����AB��ͬ������������ֱ�������Ρ�ACD�͡�BCE����ôDE������Сֵ��______________��

 4
���������������⣬����ֱ�������ε����ʣ�ƽ�Ƕ��壬���ɶ��������κ�������ֵ��
��AC��x����BC��2��x��
�ߡ�ACD�͡�BCE���ǵ���ֱ�������Σ�
���DCA��45�㣬��ECB��45�㣬DC����CE����
���DCE��90�㡣
��DE2��DC2��CE2������2��[]2��x2��2x��2��(x��1)2��1��
�൱x��1ʱ��DE2ȡ����Сֵ��DEҲȡ����Сֵ...
4
���������������⣬����ֱ�������ε����ʣ�ƽ�Ƕ��壬���ɶ��������κ�������ֵ��
��AC��x����BC��2��x��
�ߡ�ACD�͡�BCE���ǵ���ֱ�������Σ�
���DCA��45�㣬��ECB��45�㣬DC����CE����
���DCE��90�㡣
��DE2��DC2��CE2������2��[]2��x2��2x��2��(x��1)2��1��
�൱x��1ʱ��DE2ȡ����Сֵ��DEҲȡ����Сֵ... ���κ���y=x2��2x+6����Сֵ��____��
 5
�����������������y=x2��2x+6=x2��2x+1+5
=��x��1��2+5��
�ɼ������κ�������СֵΪ5��
5
�����������������y=x2��2x+6=x2��2x+1+5
=��x��1��2+5��
�ɼ������κ�������СֵΪ5�� ��ͼ����֪�ȱߡ�AEB�͵ȱߡ�BDC���߶�ACͬ�࣬�����������ǣ�������
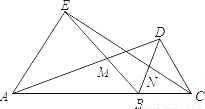
A. ��ABD�ա�EBC B. ��NBC�ա�MBD C. DM=DC D. ��ABD=��EBC
 C
��������ѡ��A����������SAS��֤����ȷ��ѡ��B����������AAS��֤����ȷ��ѡ��C����֤��MBN=60�㣬��DM=DC=DB�����DMBΪ�ȱ������Σ�����BDM=60�㣬�ߡ�EAB=��DBC����AE��BD�����BDM=��EAD=60�㣮����֪����������ѡ��D�����ɡ�ABE����DBCͬ��һ����DBE�õ�����ȷ.���Դ�����ǵ�����,��ѡC.
C
��������ѡ��A����������SAS��֤����ȷ��ѡ��B����������AAS��֤����ȷ��ѡ��C����֤��MBN=60�㣬��DM=DC=DB�����DMBΪ�ȱ������Σ�����BDM=60�㣬�ߡ�EAB=��DBC����AE��BD�����BDM=��EAD=60�㣮����֪����������ѡ��D�����ɡ�ABE����DBCͬ��һ����DBE�õ�����ȷ.���Դ�����ǵ�����,��ѡC. ��֪һֱ�DZߺ�����ֱ�DZߵĶԽǣ�����ֱ��������(�ó߹���ͼ����д��������Ҫ������ͼ�ۼ�)��
 ������
�������������������������д����֪��������Ȼ���ٻ���ͼ�μ��ɣ�
�����������֪���߶�a�͡Ϧ�������ͼ(1).
������Rt��ABC��ʹBC=a����C=90?����A=�Ϧ�.
������(1)���Ϧ�����ǡϦ�.
(2)����MBN=�Ϧ�.
(3)������BM�Ͻ�ȡBC=a.
(4)����C��CA��BM����BN�ڵ�A����ͼ(2).
��ABC���������ֱ��������...
������
�������������������������д����֪��������Ȼ���ٻ���ͼ�μ��ɣ�
�����������֪���߶�a�͡Ϧ�������ͼ(1).
������Rt��ABC��ʹBC=a����C=90?����A=�Ϧ�.
������(1)���Ϧ�����ǡϦ�.
(2)����MBN=�Ϧ�.
(3)������BM�Ͻ�ȡBC=a.
(4)����C��CA��BM����BN�ڵ�A����ͼ(2).
��ABC���������ֱ��������... ��Rt��ABC�У���ǡ�A��ƽ��������ǡ�B��ƽ�����ཻ�ڵ�D�����ADB��______��
 135��
����������Rt��ABC��,��CAB+��CBA=180��?90��=90�㣬
����ǡ�A��ƽ��������ǡ�B��ƽ�����ཻ�ڵ�D��
���DAB+��DBA= (��CAB+��CBA)= ��90��=45�㣬
�ڡ�ABD��,��ADB=180��?(��DAB+��DBA)=180��?45��=135��
�ʴ�Ϊ��135��.
135��
����������Rt��ABC��,��CAB+��CBA=180��?90��=90�㣬
����ǡ�A��ƽ��������ǡ�B��ƽ�����ཻ�ڵ�D��
���DAB+��DBA= (��CAB+��CBA)= ��90��=45�㣬
�ڡ�ABD��,��ADB=180��?(��DAB+��DBA)=180��?45��=135��
�ʴ�Ϊ��135��. ����������һ�㣬�������ߵľ�����ȣ�������Ǹ������ε�(����)
A. �������߽��� B. ������ƽ���߽���
C. �������߽��� D. ������������ֱ�߽���
 B
�����������������ν�ƽ�����ϵĵ㵽�ǵ����ߵľ�����ȿɵô˵�Ϊ��ƽ���ߵĽ���.
��ѡ��B.
B
�����������������ν�ƽ�����ϵĵ㵽�ǵ����ߵľ�����ȿɵô˵�Ϊ��ƽ���ߵĽ���.
��ѡ��B. ��֪����ʽx2��a����ƽ���ʽ����������Χ�ڷֽ���ʽ����ô�������ĸ�����a���Ե���( )
A. 9 B. 4
C. ��1 D. ��2
 C
����������x=-1ʱ��x2-1=��x+1����x-1��������������ѡ�������Ҫ��ѡC.
C
����������x=-1ʱ��x2-1=��x+1����x-1��������������ѡ�������Ҫ��ѡC. �����κ���y=ax2-2ax+c��ͼ����(-1,0),��ax2-2ax+c=0�Ľ�Ϊ (����)
A. x1=-3,x2=-1 B. x1=1,x2=3 C. x1=-1,x2=3 D. x1=-3,x2=1
 C
�������������������������ɵã����κ����ĶԳ���Ϊֱ��x=1��������x��Ľ�������Ϊ(��1��0)��(3��0)���̵Ľ�Ϊx=��1��x=3.
C
�������������������������ɵã����κ����ĶԳ���Ϊֱ��x=1��������x��Ľ�������Ϊ(��1��0)��(3��0)���̵Ľ�Ϊx=��1��x=3. 
