题目内容
13.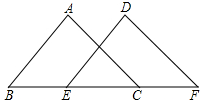 如图,点B、E、C、F在同一条直线上,∠A=∠D,AB∥DE,BE=CF,求证:AC∥DF.
如图,点B、E、C、F在同一条直线上,∠A=∠D,AB∥DE,BE=CF,求证:AC∥DF.
分析 证明△ABC≌△DEF,根据全等三角形的对应角相等证明∠ACB=∠F,然后根据平行线的判定定理证明.
解答 证明:∵AB∥DE,
∴∠B=∠DEF,
∵BE=CF,
∴BC=EF,
∴在△ABC和△DEF中,$\left\{\begin{array}{l}{∠A=∠D}\\{∠B=∠DEF}\\{BC=EF}\end{array}\right.$,
∴△ABC≌△DEF,
∴∠ACB=∠F,
∴AC∥DF.
点评 本题主要考查三角形全等的判定和全等三角形的对应角相等,要牢固掌握并灵活运用这些知识.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
3. 如图所示,已知O是直线AB上一点,∠1=38°,OD平分∠BOC,则∠2的度数是( )
如图所示,已知O是直线AB上一点,∠1=38°,OD平分∠BOC,则∠2的度数是( )
 如图所示,已知O是直线AB上一点,∠1=38°,OD平分∠BOC,则∠2的度数是( )
如图所示,已知O是直线AB上一点,∠1=38°,OD平分∠BOC,则∠2的度数是( )| A. | 19° | B. | 52° | C. | 71° | D. | 142° |
8.下列计算中,正确的是( )
| A. | 3a+2b=5ab | B. | 7ab-4ba=0 | C. | 4x2y-3xy2=x2y | D. | 3x2+5x2=8x2 |
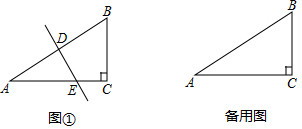
 已知:如图,P、Q是△ABC边BC上两点,且AB=AC,AP=AQ.求证:BP=CQ.
已知:如图,P、Q是△ABC边BC上两点,且AB=AC,AP=AQ.求证:BP=CQ.